Question

A bird is perched on the top of a tree 30m high and its elevation from the point on the ground is $ 45{}^\circ $ . It flies off horizontally straight away from the observer and in 2 seconds the elevation of the bird is reduced to $ 30{}^\circ $ . The speed of the bird in m/s is:
(a) 14.64
(b) 21.96
(c) 10.98
(d) 12

Answer 1

Hint: Start by letting the speed of the bird be x m/s. So, the distance travelled in 2 sec is 2x meters. Also, focus on the point that the bird is sitting at a height of 30m and consider the distance between the trees and the observer to be y meters. After that use the value of $ \tan 45{}^\circ $ and the basic definition of $ \tan \theta =\dfrac{perpendicular}{base} $ and get the value of y. In the case after the bird flew for 2 seconds, angle of elevation is $ 30{}^\circ $ , base is y+2x and height is the same. Use the value of $ \tan 30{}^\circ $ and hence, get the value of y+2x. Use the two results to reach the answer.

Complete step-by-step answer:
Let the speed of the bird be x m/s. Also, the distance between the tree and the observer is y meters.
As we know that the distance is the product of speed and time. So, the distance travelled by a bird in 2 seconds is 2x meters.
Now we will draw the diagram of the situations according to assumed and given data.

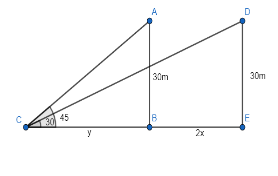
Let us first look at the triangle ABC.
In $ \Delta ABC $ , it is given that $ \angle ACB=45{}^\circ $ . We also know that $ \tan \theta =\dfrac{perpendicular}{base} $ .
 $ \tan (\angle ACB)=\dfrac{AB}{BC} $
 $ \Rightarrow \tan 45{}^\circ =\dfrac{30}{y} $
We know that the value of $ \tan 45{}^\circ =1 $ .
 $ 1=\dfrac{30}{y} $
 $ \Rightarrow y=30m.......(i) $
Now we will move to triangle DCE.
In $ \Delta DCE $ , it is given that $ \angle DCE=30{}^\circ $ . We also know that $ \tan \theta =\dfrac{perpendicular}{base} $ .
 $ \tan (\angle DCE)=\dfrac{DE}{EC} $
 $ \Rightarrow \tan 30{}^\circ =\dfrac{30}{y+2x} $
We know that the value of $ \tan 30{}^\circ =\dfrac{1}{\sqrt{3}} $ .
 $ \dfrac{1}{\sqrt{3}}=\dfrac{30}{y+2x} $
 $ \Rightarrow y+2x=30\sqrt{3} $
Now, we will substitute the value of y from equation (i). On doing so, we get
 $ 30+2x=30\sqrt{3} $
 $ \Rightarrow 2x=30\sqrt{3}-30 $
 $ \Rightarrow x=15\sqrt{3}-15 $
Now, we will put $ \sqrt{3}=1.73 $ . On doing so, we get
 $ x=15\left( \sqrt{3}-1 \right)=15\left( 1.73-1 \right)=15\times 0.73=10.95\text{ }m/s $
The closest option to our answer is option (c). Hence, the answer to the above question is option (c).

Note: Do not use any other trigonometric function like sine or cosine of the given angle because the information which is provided to us is related to the base of the triangle and the height. So, the length of the hypotenuse is of no use. Therefore, the formula of the tangent of the angle is used. We can use sine or cosine of the given angles but then the process of finding the height will be lengthy.