Question

A bird is flying with a speed of \[40km/h\] in the north direction. A train is moving with a speed of \[40km/h\] in the west distance. A passenger sitting in the train will see the bird moving with velocity
A. \[40km/h\] in N-E direction
B. \[40\sqrt 2 km/h\] in N-E direction
C. \[40km/h\] in N-W direction
D. \[40\sqrt 2 km/h\] in N-W direction

Answer 1

Hint: Motion is defined as the change in position of an object as a variation of time. The relative velocity plays an important role in the study of kinematics.
In the question, the relative motion of the bird with respect to the train is asked. Bird is flying in the north direction and the train is moving in the west direction.
Then direction and speed of the bird seen by the passenger in the train is calculated by phenomena of resultant vectors. The direction of the first vector is north and the direction of the second vector is west. So we are using a vector addition formula to calculate the resultant vector.

Complete step by step answer:Given: velocity of bird, \[{\overrightarrow v _b} = 40km/h\] in direction of north, velocity of train, \[{\overrightarrow v _t} = 40km/h\] in direction of west
Let velocity of train = \[ - {\overrightarrow v _t}\] , i.e train superimpose velocity on both the objects.
The bird possesses two velocities: velocity towards north= \[{\overrightarrow v _b}\] and velocity towards East=\[ - {\overrightarrow v _t}\].
Hence, resultant velocity of bird with respect to train is given by \[{\overrightarrow v _R}\]
\[\left| {{{\overrightarrow v }_R}} \right| = \sqrt {{{\left| {{{\overrightarrow v }_b}} \right|}^2} + {{\left| { - {{\overrightarrow v }_t}} \right|}^2}} \] [ resultant velocity \[{\overrightarrow v _R}\] of two velocities when angle between them , i.e.\[\theta = {90^0}\]]

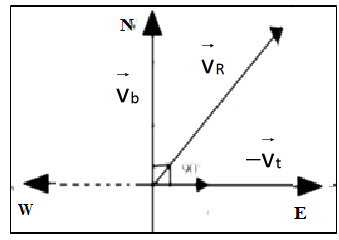
\[\Rightarrow \left| {{{\overrightarrow v }_R}} \right| = \sqrt {{{40}^2} + {{\left( { - 40} \right)}^2}} \]
\[\Rightarrow \left| {{{\overrightarrow v }_R}} \right| = 40\sqrt 2 \]\[km{h^{ - 1}}\]
\[\Rightarrow \tan \theta = \dfrac{{40}}{{40}} = 1\]
\[\Rightarrow \theta = {45^0}\]
So. the direction of the bird is viewed by the passenger and is seen toward the North-East.
Hence, option (B) is correct.

Additional information: Relative speed and Relative velocities seem similar but both of them are two different quantities. Relative speed is defined by the speed of a moving object with respect to another. Relative speed is given by difference and addition of two velocities when two bodies are moving in the same and opposite direction.

Note:On solving questions, students must be careful of taking direction of two moving objects. The best way to choose appropriate direction and for that they should draw diagrams to calculate the correct value of relative motion.