Question

A bird flies in a circle on a horizontal plane. An observer stands at a point on ground. Suppose ${{60}^{\circ }}$ and ${{30}^{\circ }}$ are the maximum and the minimum angles of elevation of the bird and that they occur when the bird is at the points P and Q respectively. Let $\theta $ be the angle of elevation of the bird when it is at a point on arc of the circle exactly midway between P and Q. find the numerical value of \[{{\tan }^{2}}\theta \] (Assume that the observer is not inside the vertical projection)

Answer 1

Hint: Now we are given ${{60}^{\circ }}$ and ${{30}^{\circ }}$ are the maximum and the minimum angles of elevation of the bird and that they occur when the bird is at the points P and Q respectively. Let us take P’ and Q’ as the projection of points on ground. Let the observer be at point A. Hence we will draw right angles triangles APP’ and AQQ’. Now take the tangent ratio for the two known angles. Note that the height will remain constant and just the horizontal distance or the adjacent sides will change. Now we will take the tan ratio at the unknown angle $\theta $ when the bird is at position R which is in centre of P and Q on circular trajectory. In the expression of $\theta $ we will substitute the values obtained from above equations to find ${{\tan }^{2}}\theta $

Complete step by step answer:
Now it is given that a bird flies in a circle on a horizontal plane and the observer stands at a point on ground outside the vertical projection of the bird’s trajectory. The maximum elevation of the bird is ${{60}^{\circ }}$ and occurs when the bird is at point P. The minimum angle of elevation is ${{30}^{\circ }}$ and occurs when the bird is at point Q and $\theta $ be the angle of elevation of the bird when it is at a point on arc of the circle exactly midway between P and Q. Now let us draw a diagram with the given data.

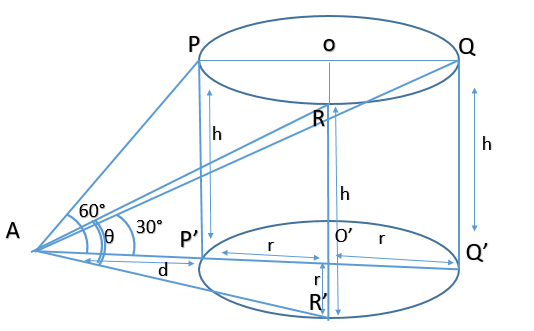
Now first consider the triangle APP’.
In the triangle we know that AP’ = d, PP’ = h and angle PAP’ = 60 degrees.
Now we know that $\tan \theta =\dfrac{\text{Opposite side}}{\text{Adjacent side}}$ . Hence taking the tan ratio on angle PAP’ we get.
$\tan {{60}^{\circ }}=\dfrac{PP'}{AP'}=\dfrac{h}{d}$
But we know that \[\tan {{60}^{\circ }}=\sqrt{3}\] substituting we get
\[\dfrac{h}{d}=\sqrt{3}...................................\left( 1 \right)\]
Now consider triangle QAQ’
Now from the figure we have AQ’ = AP’ + P’O’ + O’Q’
Hence we have AQ’ = d + r + r = d + 2r.
Hence we have AQ’ = d + 2r.
Now we know that the triangle we have QQ’ = h, $\angle QAQ'={{30}^{\circ }}$ and AQ’ = d + 2r.
Now we know that$\tan \theta =\dfrac{\text{Opposite side}}{\text{Adjacent side}}$ . Hence taking the tan ratio on angle QAQ’ we get.
\[\tan {{30}^{\circ }}=\dfrac{QQ'}{AQ'}=\dfrac{h}{\left( d+2r \right)}\]
Now we know that $\tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}}$
Hence we get
$\dfrac{1}{\sqrt{3}}=\dfrac{h}{\left( d+2r \right)}...............................\left( 2 \right)$
Now again from the figure we have
P’Q’ = A’Q’ – A’P’
2r = (d + 2r) – (d)
Now again substituting values from equation (1) and equation (2) we get.
$\begin{align}
  & 2r=\left( h\sqrt{3} \right)-\dfrac{h}{\sqrt{3}} \\
 & \Rightarrow 2r=\dfrac{h\sqrt{3}\sqrt{3}-h}{\sqrt{3}} \\
 & \Rightarrow 2r=\dfrac{3h-h}{\sqrt{3}} \\
 & \Rightarrow 2r=\dfrac{2h}{\sqrt{3}} \\
 & \Rightarrow \dfrac{r}{h}=\dfrac{1}{\sqrt{3}}...................................\left( 3 \right) \\
\end{align}$
Now consider triangle AO’R’.
Now in this triangle with Pythagoras theorem we have
$\begin{align}
  & O'{{A}^{2}}+O'{{R}^{2}}=R'{{A}^{2}} \\
 & \Rightarrow {{\left( d+r \right)}^{2}}+{{r}^{2}}={{\left( R'A \right)}^{2}} \\
 & \Rightarrow \left( R'A \right)=\sqrt{{{\left( d+r \right)}^{2}}+{{r}^{2}}} \\
\end{align}$
Now consider triangle RAR’
In this triangle we have RR’ = h, $\angle RAR'=\theta $ and $\left( R'A \right)=\sqrt{{{\left( d+r \right)}^{2}}+{{r}^{2}}}$
Hence we get
\[\tan \theta =\dfrac{RR'}{R'A}=\dfrac{h}{\sqrt{{{\left( d+r \right)}^{2}}+{{r}^{2}}}}\]
Now we know that $\tan \theta =\dfrac{1}{\cot \theta }$ using this we get.
\[\cot \theta =\dfrac{\sqrt{{{\left( d+r \right)}^{2}}+{{r}^{2}}}}{h}\]
Now squaring on both sides we get
\[{{\cot }^{2}}\theta =\dfrac{{{\left( d+r \right)}^{2}}+{{r}^{2}}}{{{h}^{2}}}\]
Now we will try to rearrange the terms as to get it in the form of $\left( \dfrac{d+2r}{h} \right)$ , $\left( \dfrac{d}{h} \right)$and $\left( \dfrac{r}{h} \right)$
Now first using the formula ${{\left( a+b \right)}^{2}}={{a}^{2}}+{{b}^{2}}+2ab$ we get
\[{{\cot }^{2}}\theta =\dfrac{\left( {{d}^{2}}+2dr+{{r}^{2}} \right)+{{r}^{2}}}{{{h}^{2}}}\]
Hence we get
\[\begin{align}
  & {{\cot }^{2}}\theta =\dfrac{{{d}^{2}}+2dr+2{{r}^{2}}}{{{h}^{2}}} \\
 & \Rightarrow {{\cot }^{2}}\theta =\dfrac{{{d}^{2}}+2dr}{{{h}^{2}}}+\dfrac{2{{r}^{2}}}{{{h}^{2}}} \\
 & \Rightarrow {{\cot }^{2}}\theta =\dfrac{d(d+2r)}{{{h}^{2}}}+\dfrac{2{{r}^{2}}}{{{h}^{2}}} \\
 & \Rightarrow {{\cot }^{2}}\theta =\dfrac{d}{h}\left( \dfrac{d+2r}{h} \right)+2{{\left( \dfrac{r}{h} \right)}^{2}} \\
\end{align}\]
Now substituting the values from equation (1), equation (2) and equation (3) we get
\[{{\cot }^{2}}\theta =\sqrt{3}\times \dfrac{1}{\sqrt{3}}+2{{\left( \dfrac{r}{h} \right)}^{2}}\]
Hence we get
\[{{\cot }^{2}}\theta =1+\dfrac{2}{3}\]
\[{{\cot }^{2}}\theta =\dfrac{3+2}{2}=\dfrac{5}{3}\]
Now we know that $\tan \theta =\dfrac{1}{\cot \theta }$ using this we get.
${{\tan }^{2}}\theta =\dfrac{3}{5}$

Hence the value of \[{{\tan }^{2}}\theta =\dfrac{3}{5}\] .

Note: Now note that the angles RAR’ and ROR’ are the same and hence both the angles are $\theta $ they are just the same angles lying in different planes in the third dimension. Refer to the diagram to understand this better. Also here note that we had height and adjacent sides of angles and hence we preferred to take tan ratio. Similarly for such problems always note the data to choose the correct trigonometric ratio.