Question

A bearing mounted in a pillow block housing experiences forces as shown below.

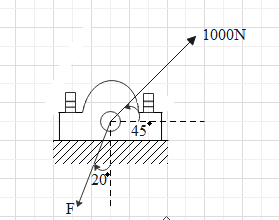
What should be magnitude of F, in order to minimise the resultant force.

Answer 1

Hint: Here we have given a bearing which experiences force of 1000N and F. We have to find the value of F such that the resultant force is minimised. To find the value of F we can redraw the above diagram for the forces and its components. By balancing the forces we can calculate the value of F.
Formula used:
\[R=\sqrt{{{A}^{2}}+{{B}^{2}}}\]

Complete answer:
Let us redraw the above diagram for the forces and the components associated with it.

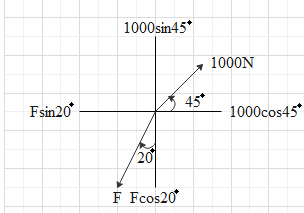
Now here we can see that 1000N force will have two components of sine and cosine. Similarly, force F will also have sin and cosine components. Now the cosine component of the 1000N force is balancing the sine component of F and the sine component of 1000N force is balancing the cosine component of F. Hence, by balancing the forces we will get two equation and so two values of F. and with F we can find the magnitude of F such that resultant force is minimised.
By balancing the forces from above diagram we get
\[\begin{align}
  & F\sin 20{}^\circ =1000\cos 45{}^\circ \\
 & F\cos 20{}^\circ =1000\sin 45{}^\circ \\
\end{align}\]
Let us solve each equation one-by-one and find the value of F.
\[\begin{align}
  & F\sin 20{}^\circ =1000\cos 45{}^\circ \\
 & \Rightarrow F=\dfrac{1000\cos 45{}^\circ }{\sin 20{}^\circ } \\
 & \Rightarrow F=\dfrac{1000\times 0.707}{0.342} \\
 & \Rightarrow F=\dfrac{707}{0.342} \\
 & \Rightarrow F=2067.25N \\
\end{align}\]
Similarly, solving second equation, we get
\[\begin{align}
  & F\cos 20{}^\circ =1000\sin 45{}^\circ \\
 & \Rightarrow F=\dfrac{1000\sin 45{}^\circ }{\cos 20{}^\circ } \\
 & \Rightarrow F=\dfrac{1000\times 0.707}{0.940} \\
 & \Rightarrow F=\dfrac{707}{0.94} \\
 & \Rightarrow F=752.12N \\
\end{align}\]
We got two values of F or the bearing.
Now resultant force is given by the following formula
\[R=\sqrt{{{A}^{2}}+{{B}^{2}}}\]
If A is 1000N force and B is F, then we can see that F is directly proportional to R. Therefore if F increases, R increases and if F decreases, R decreases.
So, we get the minimum value of R for \[F=752.12N\].

Hence the bearing should be designed in such a way that the value of force F is 752.12N.

Note:
We can also substitute the values and verify the result instead of using the proportionality. But the figures are large (having a place value of a thousand) and their squaring will give us a much larger digit and calculation will get complicated. Therefore we use the proportionality instead substituting values.