Question

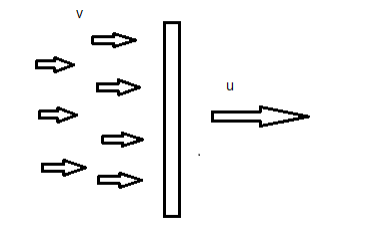
A beam of gas molecules is incident normally on a plate AB. Each gas molecule has mass $m$ and velocity $v$ . The incident beam falls on an area A on the plate and all the molecules strike the plate elastically. Number of molecules in the unit volume of the beam is $n$. When the plate is moved to the right a force $F_{1}$ is needed to keep it moving with constant velocity $u(

\[\begin{align}
  & A.8mAnvu \\
 & B.6mAnuv \\
 & C.4mAnuv \\
 & D.3mAnuv \\
\end{align}\]

Answer 1

Hint: A elastic collision occurs when the total kinetic energy of the two bodies interacting bodies is conserved. Here, we can consider the interaction of the molecules with the plate to be in one direction and solve the following.
Formula: $F=N\times \Delta p$

Complete answer:
Let us assume that the given plate is moving towards the right as shown in the figure with a velocity $u$, then the particles, which are bombarding the plate with a velocity $v$ will get reflected back towards the left with some velocity $v\prime$.
Since it is given that the particle undergoes elastic collision, we can say that the coefficient of restitution $e=1$.
Then, here, we have $1=\dfrac{u-(-v\prime)}{v-u}$
$\implies v\prime+u=v-u$
$\implies v\prime=v-2u$
Then the change in momentum is given as $\Delta p=mv\prime-(-mv)$
$\implies \Delta p=m(v-2u)+mv$
$\implies \Delta p=2(mv-mu)$
Let us consider the number moles of the molecules which hit the plate per unit time, it is given as $N=nAv=nA(v-u)$, where $n$ is the number of moles, which are incident on area $A$ of the plate.
Then the force $F_{1}$ acting on the plate is given as $F_{1}=N\times \Delta p$
$\implies F_{1}=nA(v-u)\times 2m(v-u)$
$\implies F_{1}=2mnA(v-u)^{2}$
Similarly, the force $F_{2}$ due to which the plate moves to the left with a velocity $u$, then the particles, which are bombarding the plate with a velocity $v$ will get reflected back towards the left with the some velocity $v\prime\prime$.
Then, again, since the collision is elastic, we can say that, $e=1=\dfrac{v\prime\prime-u}{v-(-u)}$
$\implies v+u=v\prime\prime- u$
$\implies v\prime\prime=v+2u$
Then, the change in momentum is given as $\Delta p=mv\prime\prime-(-mv)$
$\implies \Delta p=m(v+2u)+mv$
$\implies \Delta p=2(mv+mu)$
Then the number moles of the molecules which hit the plate per unit time, it is given as $N=nAv=nA(v+u)$
Then the force $F_{2}$ acting on the plate is given as $F_{2}=N\times \Delta p$
$\implies F_{2}=nA(v+u)\times 2m(v+u)$
$\implies F_{1}=2mnA(v+u)^{2}$
Then $F_{1}-F_{2}=2mnA[(v+u)^{2}-(v-u)^{2}]$
$\implies F_{1}-F_{2}=2mnA[(v+u-(v-u))(v+u+(v-u))]$
$\implies F_{1}-F_{2}=2mnA[(v+u-v+u)(v+u+v-u)]$
$\implies F_{1}-F_{2}=2mnA[(2u)(2v)]$
$\therefore F_{1}-F_{2}=8mnAuv$

Hence the correct option is \[A.8mAnvu\]

Note:
We know that coefficient of restitution is defined as the ratio between the velocity after collision to the velocity before collision. It is given as\[\text{e=}\dfrac{\text{relative velocity after collision}}{\text{relative velocity before collision}}\]. Here we are considering two situations, when the plate is moving towards left and right. Then using the two we can find the respective forces.