Question

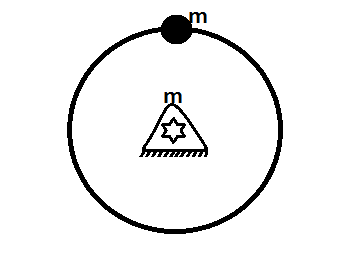
A bead of mass $m$ is welded at the periphery of the smoothly pivoted disc of mass m and radius $R$ as shown in figure. The pivot axis is horizontal and through the centre of the disc. The disc is free to rotate in a vertical plane. The disc is released from rest from the position shown. Find the speed of the bead at its lowest position?
$(A)\sqrt {\left( {\dfrac{3}{8}} \right)gR} $
$(B)\sqrt {\left( {\dfrac{3}{4}} \right)gR} $
$(C)\sqrt {\left( {\dfrac{4}{3}} \right)gR} $
$(D)\sqrt {\left( {\dfrac{8}{3}} \right)gR} $

Answer 1

Hint:This question is based on the concept of the law of conservation of energy. In order to find the speed of the bead at the lowest position, we will equate the kinetic energy to the potential energy. Also, to solve this question we must know that expression for the moment of inertia of the uniform mass disk concerning the rotation pivot.

Complete step by step answer:
The expression for the potential energy, relative to the lowest path position is,
$U = 2Rmg$
We also know that the expression for the kinetic energy is,
$K = \dfrac{1}{2}m{v^2} + \dfrac{1}{2}{J_o}{(\theta )^2}.......(1)$
In the above expression,
${J_o}$ is the moment of inertia of a uniform mass disk concerning the rotation pivot
The value of ${J_o}$ is given by,
${J_o} = \dfrac{1}{2}m{R^2}$
We also know that the value of $v$ is given by,
$v = \theta R$
On putting these values in the equation (1), we get,
$K = \dfrac{1}{2}m{v^2} + \dfrac{1}{2}\left( {\dfrac{1}{2}m{R^2}} \right)\dfrac{{{v^2}}}{{{R^2}}}$
According to the concept of the law of conservation of energy, the potential energy is equal to the kinetic energy while the transformation of energy takes place from one form to another form, so,
$U = K$
On putting the required values of potential energy and kinetic energy, we get,
$2Rmg = \dfrac{1}{2}m{v^2} + \dfrac{1}{2}\left( {\dfrac{1}{2}m} \right){v^2}$
On further solving, we get,
$2Rmg = \dfrac{1}{2}m{v^2} + \dfrac{1}{4}m{v^2}$
On cancelling $m$ on both the sides,
$2Rg = \dfrac{1}{2}{v^2} + \dfrac{1}{4}{v^2}$
$2Rg = \dfrac{3}{4}{v^2}$
On taking ${v^2}$ on the LHS and all the other terms on the RHS, we get,
${v^2} = \dfrac{8}{3}Rg$
On taking square root on both the sides, we get,
$v = \sqrt {\dfrac{8}{3}Rg} $
So, the speed of the bead at its lowest position is $v = \sqrt {\dfrac{8}{3}Rg} $.
Thus, the final answer is $(D)\sqrt {\left( {\dfrac{8}{3}} \right)gR} $

Note:The moment of inertia is defined as the ability of a body to remain in a state of rest or moving with the constant velocity. So, we can say that, greater the inertia of a body the greater is, the more is the force required to interrupt its present state. It is important to note that the mass of a body is equal to its linear inertia.