Question

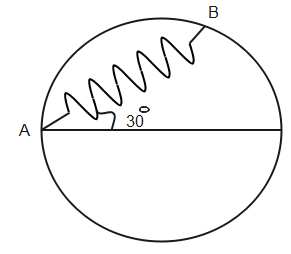
A bead of mass $m$ is attached to one end of the spring of natural length $R$ and spring constant $K=\dfrac{(\sqrt{3}+1)mg}{R}$. The other end of the spring is fixed at point A on a smooth vertical ring of radius $R$ as shown in fig. The normal reaction at B just after it is released to move is
(A). $\dfrac{mg}{2}$
(B). $\sqrt{3}mg$
(C). $3\sqrt{3}mg$
(D). $\dfrac{3\sqrt{3}mg}{2}$

Answer 1

Hint: When the bead is at point B the forces acting on it will be the force of gravity, normal force due to spring and the restoring force of the spring. The spring is under extension due to which the restoring force comes into play. The Resolving the forces and equating them and using the equations formed, we can calculate the normal reaction

Formulas used:
$F=KX$
$X=\sqrt{3}R-R$
$N=F\cos 30+mg\cos 30$

Complete step by step answer:

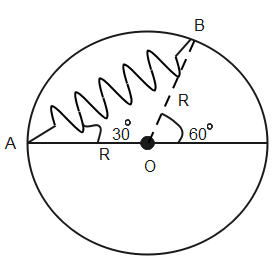
The FBD diagram of the bead is given in the figure given below

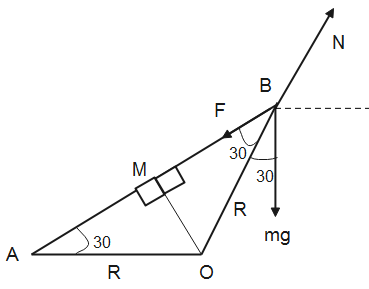
In $\Delta AOM$ and $\Delta BOM$,
$\begin{align}
  & AM=BM=R\cos 30 \\
 & \Rightarrow AM=BM=\dfrac{\sqrt{3}}{2}R \\
\end{align}$
The spring is stretched and hence its length is extended. Given, $R$ is the original length of the spring.
Therefore, the length of the spring after extension will be
$\begin{align}
  & AM+BM=\dfrac{\sqrt{3}}{2}\times 2\times R \\
 & \Rightarrow AM+BM=\sqrt{3}R \\
\end{align}$
The extension in the wire will be-
$X=\sqrt{3}R-R=(\sqrt{3}-1)R$
In the above figure,
The restoring force developed in the spring is $F$,
$F=KX$
Given, $K=\dfrac{(\sqrt{3}+1)mg}{R}$, $X=(\sqrt{3}-1)R$ substituting given values in the above equation, we get,
$\begin{align}
  & F=KX \\
 & \Rightarrow F=\dfrac{(\sqrt{3}+1)mg}{R}\times (\sqrt{3}-1)R \\
\end{align}$
$\therefore F=2mg$ - (2)
Resolving the forces into its perpendicular components, we get,

Therefore, the figure above shows us that,
$N=F\cos 30+mg\cos 30$
Substituting from eq (2),
$\begin{align}
  & N=2mg\times \dfrac{\sqrt{3}}{2}+mg\times \dfrac{\sqrt{3}}{2} \\
 & \Rightarrow N=\dfrac{3\sqrt{3}}{2}mg \\
\end{align}$
The normal force acting on the bead is $\dfrac{3\sqrt{3}}{2}mg$.
Therefore, the normal force acting on the bead when it just starts to slip from point B is $\dfrac{3\sqrt{3}}{2}mg$.

So, the correct answer is “Option D”.

Note: The spring shows harmonic motion therefore, the restoring force is proportional to the negative of displacement. The normal force is a force which two surfaces in contact exert on each other in order to stop them from passing through. The FBD diagram shows all the forces acting on a system.