Question

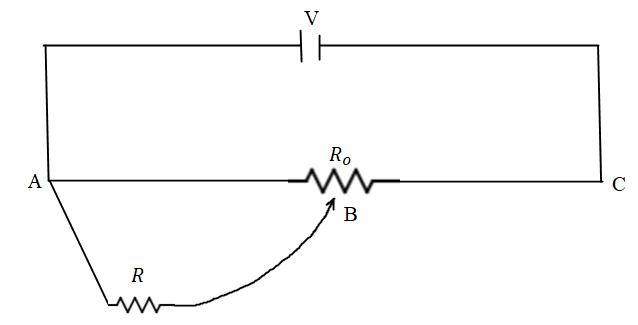
A battery of V voltage is connected across the potentiometer wire AC of total resistance ${R_o}$ as shown. Calculate the potential across the resistance R if the sliding contact point B is exactly at the middle of the potentiometer wire.

A.$\dfrac{{2VR}}{{4{R_o} + R}}$.
B.$\dfrac{{4V{R_o}}}{{2{R_o} + R}}$.
C.$\dfrac{{2VR}}{{{R_o} + 4R}}$.
D.$\dfrac{{4V{R_o}}}{{{R_o} + 2R}}$

Answer 1

Hint: A potentiometer is a device that is used to calculate the voltage difference. The resistance of the potentiometer is proportional to the length between the point A and B. The total resistance of the potentiometer is in parallel combination.

Complete answer:
The resistance between the points A and B is proportional to the length between the two points. As the length of resistance is exactly middle of the resistance between the points A and B therefore the resistance is$\dfrac{{{R_o}}}{2}$.
The resistance R and the resistance between the points A and B is $\dfrac{{{R_o}}}{2}$ and they are arranged in the parallel combination.
Let us calculate the equivalent resistance of the parallel combination,
$ \Rightarrow \dfrac{1}{{{R_1}}} = \dfrac{1}{R} + \dfrac{1}{{\left( {\dfrac{{{R_o}}}{2}} \right)}}$
Solving we get the value of ${R_1}$,
$ \Rightarrow {R_1} = \dfrac{{R \cdot {R_o}}}{{{R_o} + 2R}}$………eq. (1)
The total resistance between the point A and point C will be in series combination and is equal to,
$ \Rightarrow {R_1} + \dfrac{{{R_o}}}{2}$.
According to ohm's law the current flowing through the circuit is equal to,
$ \Rightarrow V = I \cdot R$
$ \Rightarrow I = \dfrac{V}{{{R_1} + \left( {\dfrac{{{R_o}}}{2}} \right)}}$
$ \Rightarrow I = \dfrac{{2V}}{{2{R_1} + {R_o}}}$.........eq. (2)
The voltage of the potentiometer according to the ohms law is given by,
$ \Rightarrow {{\text{V}}_1} = I \cdot {R_1}$where ${R_1}$ is the resistance between the points A and B.
Replace the value of ${R_1}$ in the above relation from the equation (1) and equation (2).
$ \Rightarrow {{\text{V}}_1} = I \cdot {R_1}$
$ \Rightarrow {{\text{V}}_1} = \left[ {\dfrac{{2V}}{{2\left( {\dfrac{{R \cdot {R_o}}}{{{R_o} + 2R}}} \right) + {R_o}}}} \right] \cdot \left( {\dfrac{{R \cdot {R_o}}}{{{R_o} + 2R}}} \right)$
After solving the above relation we get,
$ \Rightarrow {{\text{V}}_1} = \dfrac{{2{\text{V}}R}}{{4{R_o} + R}}$

So the correct option for this problem is A.

Note:
The combination of the resistance between point A and B is in parallel connection and the total resistance of the potentiometer is in series combination. The ohm's law is advisable to remember as it is used in most of the conditions.