Question

A battery consists of an ‘n’ number of identical cells (having internal resistance ‘r’ each), which are connected in series. The terminals of the battery are short-circuited and the current I is measured. Which of the graphs shows the correct relationship between I and n?
A.

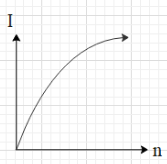
B.

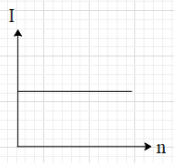
C.

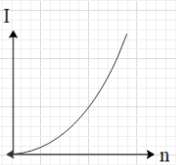
D.

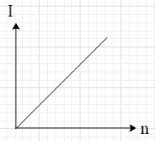
Answer 1

Hint: When n number of identical cells are connected in series, the effective emf of the n cells is equal to ${{E}_{eff}}=nE$, where E is the emf of each cell. And the effective internal resistance of the ‘n’ cells is equal to ${{r}_{eff}}=nr$, where r is the internal resistance of each cell.

Formula used:
${{E}_{eff}}=nE$
${{r}_{eff}}=nr$
$\Delta V=IR$

Complete step by step answer:
It is given that there are ‘n’ number of identical cells. Each of the cells have an internal resistance ‘r’.When a cell of some internal resistance is connected in a circuit, the potential difference produced by the cell across the component is less than its emf.It is given that the cells are connected in series. When n numbers of identical cells are connected in series, the effective emf of the n cells is equal to ${{E}_{eff}}=nE$, where E is the emf of each cell.

And the effective internal resistance of the ‘n’ cells is equal to ${{r}_{eff}}=nr$, where r is the internal resistance of each cell.This means that the n identical cells can be replaced by a single cell of emf ${{E}_{eff}}=nE$ and internal resistance ${{r}_{eff}}=nr$.It is said that the terminals of the battery are short circuited. This means that the circuit is complete and a current will flow in the circuit.
This circuit is equivalent to a circuit consisting of a cell of emf ${{E}_{eff}}=nE$ and a total resistance of ${{r}_{eff}}=nr$. From Ohm’s law we know that $\Delta V=IR$, where $\Delta V$ is a potential difference across a resistance R and I is the current in R.
Therefore,
$\Rightarrow {{E}_{eff}}=I{{r}_{eff}}$
$\Rightarrow nE=I(nr)$
$\therefore I=\dfrac{E}{r}$.
This means that current in the circuit is equal to $I=\dfrac{E}{r}$. And we know that E and r are constant. This means that the current I in the circuit is constant and is independent of n.i.e. the value of I is constant for all values of n.This is shown in the graph of option B.

Hence, the correct option is B.


Note:The formula for the effective emf of n identical in series connected is only when the opposite terminals of the cells are connected to each (i.e. the positive terminal of one cell to negative terminal of other and vice versa). In other words, the polarity of all the cells must be in the same direction. If the polarity of n cells is in one direction and the polarity of m cells is in the opposite direction, then the effective emf of the combination is equal to $nE-mE$.