Question

A baseball player with mass $ m = 79kg $ , sliding into second base, is retarded by a frictional force of magnitude 470 N. What is the coefficient of kinetic friction $ {\mu _k} $ between the player and the ground?

Answer 1

Hint: We need to construct a free body diagram, that gives the direction of forces acting on the baseball player. Equate the values given to find the net force acting in each direction. Then apply Newton’s second law of motion. Substitute the values given in the question to calculate the answer.

Formula Used: The formulae used in the solution are given here.
Force of friction $ f = {\mu _k}N $ where $ {\mu _k} $ is the coefficient of friction and $ N $ is the normal force.

Complete Step by Step Solution:
It has been given that, a baseball player with mass $ m = 79kg $ , sliding into second base, is retarded by a frictional force of magnitude 470 N.
The maximum amount of friction force that a surface can apply upon an object can be easily calculated with the use of the given formula:
 $ Friction = {\mu _k}N $ where $ {\mu _k} $ is the coefficient of kinetic friction between the player and the ground and $ N $ is the normal force.
Given that, the mass of the player $ m = 79kg $ and the force of friction between the player and the ground is $ f = 470N $ .
The free-body diagram for the player is shown below.

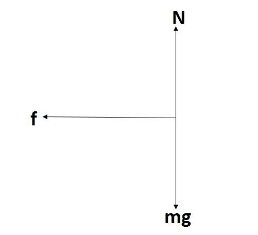
Here, $ N $ is the normal force of the ground on the player, $ mg $ is the force of gravity, and $ f $ is the force of friction.
By Newton’s second law of motion, we know that Force acting on a body is given the product of mass and acceleration. Thus, mathematically, $ F = ma $ where $ a $ is the acceleration.
We apply this law on the vertical axis. In this case, $ a = 0 $ , since the vertical component of acceleration is zero.
Thus, $ F = 0 $ .
Now, as $ F = N - mg $ , we can write,
 $ \Rightarrow N = mg $ .
Thus, the force of friction is given by, $ f = {\mu _k}N = {\mu _k}mg $ .
Substituting the values for mass and force of friction, and taking acceleration due to gravity $ g = 10m{s^{ - 2}} $ , we get,
 $ 470 = {\mu _k} \times 79 \times 10 $
 $ \Rightarrow {\mu _k} = \dfrac{{470}}{{790}} = 0.5949 $
Thus, the coefficient of kinetic friction $ {\mu _k} $ between the player and the ground is $ {\mu _k} \simeq 0.59 $ .

Note:
The value we have achieved here is solely based on the assumption that, $ g = 10m{s^{ - 2}} $ . Please note that, the value of the coefficient of kinetic friction $ {\mu _k} $ may change if the acceleration due to gravity is taken to be, $ g = 9.8m{s^{ - 2}} $ . In that case, the calculations need to be changed while the procedure remains the same.