Question

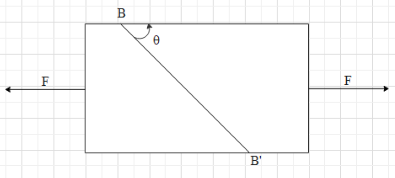
A bar of cross sectional area A is subjected to two equal and opposite tensile forces at its ends as shown in figure. Consider a plane BB’ making an angle $\theta $ with the length. The ratio of tensile stress to the shearing stress on the plane BB’ is:

A. $\tan \theta $
B. $\sec \theta $
C. $\cot \theta $
D. $\cos \theta $

Answer 1

Hint:Shear stress on the plane is equal to the ratio of the component of tension force that is along the plane to the area of the plane. Tensile stress on the plane is equal to the ratio of normal component of tension to the area of the plane.

Complete step by step answer:
The tension in the bar will be pulling the plane BB’ in the outward direction as the two forces are pulling the bar.

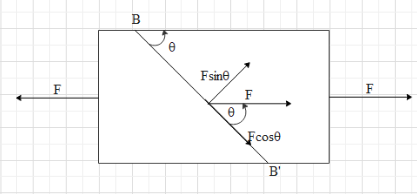
Let first calculate the shear stress on the BB’ plan BB’. Shear stress on the plane is equal to the ratio of the component of tension force that is along the plane to the area of the plane.In this case, the component of the tension parallel to the plane BB’ is equal to ${{T}_{||}}=F\cos \theta $ …. (i)
With the help of trigonometry we can write that $\sin \theta =\dfrac{A}{A'}$, where A’ is the area of the plane BB’.
Therefore, $A'=\dfrac{A}{\sin \theta }$ ….. (ii).

Now, divide (i) by (ii).
With this, we get that the shear stress on the plane BB’ is equal to ${{S}_{1}}=\dfrac{{{T}_{||}}}{A'}=\dfrac{F\cos \theta }{\dfrac{A}{\sin \theta }}$
Then,
$\Rightarrow {{S}_{1}}=\dfrac{F\sin \theta \cos \theta }{A}$ …. (iii)
Let us now find the tensile stress on the plane.
Tensile stress on the plane is equal to the ratio of normal component of tension to the area of the plane.
i.e. ${{S}_{2}}=\dfrac{{{T}_{\bot }}}{A'}$
In this case, ${{T}_{\bot }}=F\sin \theta $

Then, this means that,
${{S}_{2}}=\dfrac{{{T}_{\bot }}}{A'}=\dfrac{F\sin \theta }{\dfrac{A}{\sin \theta }}$
Therefore,
$\Rightarrow {{S}_{2}}=\dfrac{F{{\sin }^{2}}\theta }{A}$ …. (iv)
Now, divide equation (iv) by (iii).
Then,
$\Rightarrow \dfrac{{{S}_{2}}}{{{S}_{1}}}=\dfrac{\dfrac{F{{\sin }^{2}}\theta }{A}}{\dfrac{F\sin \theta \cos \theta }{A}}=\dfrac{\sin \theta }{\cos \theta }$
$\therefore\dfrac{{{S}_{2}}}{{{S}_{1}}}=\tan \theta $
This means that the ratio of tensile stress to the shearing stress on the plane BB’ is equal to $\tan \theta $.

Therefore, the correct option is A.

Note:Here, students may make a mistake in identifying which one is shear stress and which one is tensile stress. Remember that while calculating shear stress we consider the force acting along the surface and while calculating tensile stress we consider the force acting normal to the surface.