Question

A bar is subjected to equal and opposite forces as shown in the figure. PQ is a plane making an angle θ with the cross-section of the bar. If the area of cross-section is 'a', then what is tensile stress on PQ?

A. $\dfrac{F}{a}$
B. $\dfrac{{F\cos \theta }}{a}$
C. $\dfrac{{F{{\cos }^2}\theta }}{a}$
D. $\dfrac{a}{{F\cos \theta }}$

Answer 1

Hint: This question is from the part about tensile stress. A bar of cross section A is subjected to equal and opposite tensile forces F at its ends. Consider a plane through the bar making an angle θ with a plane at right angles to the bar as shown in figure.So with the help of the general equation of tensile force we get the tensile force in the plane and by resolving the force perpendicular and parallel to the plane we find the solution for the problem.

Formula used:

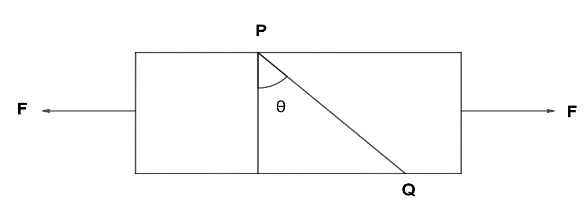
The tensile stress at this plane in terms of F, A and $\theta $ is
${\text{Tensile stress = }}\dfrac{{{\text{Normal Force}}}}{{{\text{Area}}}}$

Complete step by step answer:
Shear stress:It is defined as the restoring force acting per unit area tangential to the surface of the body.
Tensile stress: When an object is one dimensional then the force acting per unit area is called longitudinal stress. It is of two types: compressive stress and tensile stress.

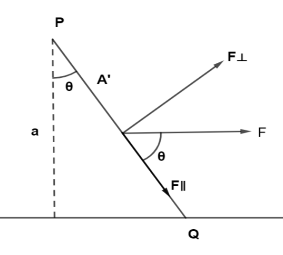
Here, $F \bot {\text{ = Fsin}}\theta $
$F\parallel {\text{ = Fsin}}\theta $
Here, produces $F \bot $ tensile stress and $F\parallel $ produces shear stress, on the plane PQ.Let A’ = area of the plane PQ
$\cos \theta {\text{ = }}\dfrac{a}{{{\text{A'}}}}$
$\Rightarrow {\text{A' = }}\dfrac{{\text{a}}}{{\cos \theta }}$

The force acting on the given plane (normal force) $F\cos \theta $. Therefore, the area along which the force acts is given by $\dfrac{a}{{\cos \theta }}$. Thus, tensile strength on the plane PQ will be:
${\text{Tensile stress = }}\dfrac{{{\text{Normal Force}}}}{{{\text{Area}}}} \\ $
$\Rightarrow {\text{Tensile stress = }}\dfrac{{{\text{Fcos}}\theta }}{{\dfrac{{\text{a}}}{{\cos \theta }}}} \\ $
$\therefore {\text{Tensile stress = }}\dfrac{{F{{\cos }^2}\theta }}{a}$

Therefore, the correct answer is option C.

Note: Here we take the area as $\dfrac{a}{{\cos \theta }}$ because we need the area of the inclined plane that is the area of the triangle formed. A force can be transmitted from one point to another point along the same line of action such that the effect produced by the force on a body remains unchanged. The net effect of a system of forces on a body is the same as that of the combined effect of individual forces on the body. The action of a force on a body is not affected by the action of any other force on the body.