Question

A banquet hall is 25 m long and 17 m broad. A carpet is laid inside the hall leaving all-around a margin of 50 cm from the walls. Find the area of the carpet and the area of the strip left uncovered. If the width of the carpet is 96 cm, then find its cost at the rate of Rs. 20 per m.

Answer 1

Hint:
We are required to find the area of the carpet, the area of strip left uncovered, and the cost of the carpet. To do that, we will find the required areas and the dimensions using the formula. Then we will use the concept of the unitary method to find the cost of the carpet.
Formula Used: We will use the formula \[{\rm\text{Area of rectangle}} = {\rm\text{length}} \times {\rm\text{breadth}}\] to solve the given question.

Complete step by step solution:
We are given that we have a banquet hall with dimensions, 25 m long and 17 m broad. The carpet on the floor is laid inside the hall leaving all-around a margin of 50 cm from the walls. Based on this given information, let us make a diagram for a better understanding.

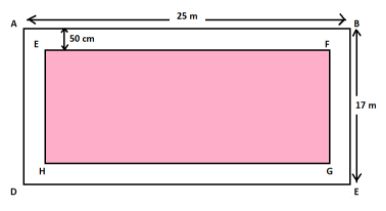
From the above figure, we can see that \[ABCD\] represents the floor of the banquet hall. Whereas, \[EFGH\] represents the carpet area.
Let us find the area of the floor first.
\[{\rm\text{Length of floor}} = 2{\rm{5 m}}\]
\[{\rm\text{Breadth of floor}} = {\rm{17 m}}\]
Since, the floor is in the shape of a rectangle its area will be, \[{\rm\text{Area of rectangle}} = {\rm\text{length}} \times {\rm\text{breadth}}\].
Substitute the values of length and breadth in the above formula to obtain the value of the area.
\[{\rm\text{Area of rectangle}} = 25 \times 17\\ = 425{\rm{ }}{{\rm{m}}^2}\]
Hence the area of the floor is \[425{\rm{ }}{{\rm{m}}^2}\].
Now we are required to find the area of the carpet.
While finding the area of the carpet we will deduct the margins from the dimensions of the floor to get the dimensions of the carpet. As the margins are on two ends, hence, the deductions of twice the margins from the dimensions of the floor will be made.
Now, we know that the margin is given as 50 cm. We will now convert 50 cm into metre.
\[50{\rm{ cm}} = \dfrac{{50}}{{100}} = 0.5{\rm{ m}}\]
Now we will calculate the length and breadth of the carpet.
\[{\rm\text{Length of the carpet}} = 25 - 2\left[ {0.5} \right]\\ = 25 - 1\\ = 24\]
\[{\rm\text{Breadth of the carpet}} = 17 - 2\left[ {0.5} \right]\\ = 17 - 1\\ = 16\]
Since, the carpet is in the shape of a rectangle its area will be, \[{\rm\text{Area of carpet}} = {\rm\text{length}} \times {\rm\text{breadth}}\].
We will substitute the values of length and breadth in the above formula to obtain the value of the area.
\[{\rm\text{Area of carpet}} = 24 \times 16\\ = 384{\rm{ }}{{\rm{m}}^2}\]
Hence the area of the carpet is \[384{\rm{ }}{{\rm{m}}^2}\].
Now, we have to find the area of the strip that is left uncovered.
\[{\rm\text{Area of strip left uncovered}} = {\rm\text{Area of floor}} - {\rm\text{Area of carpet}}\\ = 425 - 384\\ = 41{\rm{ }}{{\rm{m}}^2}\]
Hence, the area of the strip left uncovered is \[41{{\rm{m}}^2}\].
Now we have to find the cost of the carpet. It is given that the width of the carpet is 96 cm.
We will convert 96 cm into meters.
\[96{\rm{ cm}} = \dfrac{{96}}{{100}} = 0.96{\rm{ m}}\]
Now the total breadth of the carpet should be 16 m.
Hence, the total number of carpets that will be needed with the given \[0.96\] m width, to cover the total width of 16 m will be,
\[{\rm\text{Total number of carpets}} = \dfrac{{{\rm\text{Total width}}}}{{{\rm\text{Width of one carpet}}}}\\ = \dfrac{{16}}{{0.96}}\\ = 16.67\]
Hence, the total number of carpets required are \[16.67\].
\[16.67\] carpets, each of length 24 m will be needed.
Thus, the total length of the carpets will be,
\[{\rm\text{Total length of the carpet}} = {\rm\text{Total number of carpets}} \times {\rm\text{length of one carpet}}\\ = 16.67 \times 24\\ = 400.08{\rm{m}}\]
Now the cost of 1 m of carpet is given as Rs. 20.
We will now calculate the total cost
\[{\rm\text{Total cost of carpet}} = {\rm\text{Total length of carpet}} \times {\rm\text{Cost of 1m length carpet}} \\ = 400.08 \times 20 \\ = {\rm{Rs.}}8001.6\]

\[\therefore\] The total cost of the carpet will be Rs. \[8001.6\] .

Note:
We might be misled by the statement that ‘If the width of the carpet is 96 cm’. We might take this as the new width and multiply it with the length to calculate the cost of the carpet. But this is wrong, to calculate the cost we will find the number of carpets then the total length. And hence we will obtain the total cost of the carpet. Also, we need to take care of the units metre and centimeter and their conversion. As here in the question, the carpet size is given in centimeter and hall size in metre, so we need to convert either the carpet size into metre or hall size into centimetre. If the units are not converted, then we will get the wrong answer.