Question

A balloon is rising with constant acceleration $2m/{{s}^{2}}$ . Two stones are released from the balloon at the interval of 2 sec. Find out the distance between two stones 1 sec after the release of the second stone.

Answer 1

Hint: First of all we will find the net acceleration of the stones after they are released from the balloon and then we will find the individual distances covered by them in the given time using the relation, $s=ut+\dfrac{1}{2}a{{t}^{2}}$. Then on the basis of that we will find the difference between distances of the stone, hence we will get our answer.

Formula used: $s=ut+\dfrac{1}{2}a{{t}^{2}}$

Complete step by step answer:
In the question it is given that a balloon is rising with constant acceleration $2m/{{s}^{2}}$ and two stones are released from the balloon at the interval of 2 sec, so, on the basis of the given data we will draw a figure for our simplicity.

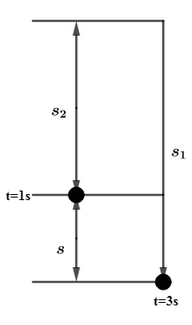
Now, from figure it can be seen that the total time taken by stone 1 to cover distance ${{s}_{1}}$ is 3 sec, meanwhile stone 2 covers ${{s}_{2}}$ distance in 1 sec as it was released at an interval of 2 sec, this can be written mathematically as,
Distance covered by the stone 1 after it was released from balloon$ = {{s}_{1}}$,
Distance covered by the stone 2 after it was released from balloon$ = {{s}_{2}}$,
Time taken by stone 1 to cover distance ${{s}_{1}}$ is ${{t}_{1}}=3\sec $, and
Time taken by stone 2 to cover distance ${{s}_{2}}$ is ${{t}_{2}}=1\sec $
Now, the acceleration of the stones 1 and 2 after they are released are the same and equal to the summation of acceleration of the balloon and gravitational acceleration acting on them when falling downwards. This can be given mathematically as,
Net acceleration of stone 1 and 2 is ${{a}_{net}}=a+g$
Now, the relation between acceleration, speed and time can be given by the relation,
$s=ut+\dfrac{1}{2}a{{t}^{2}}$ …………(i)
Where, s is distance covered, u is initial velocity, a is acceleration and t is time.
Here the initial velocity will be zero as stones are performing free fall motion. Now, distances covered by two stones can be given as,
${{s}_{1}}=u{{t}_{1}}+\dfrac{1}{2}{{a}_{1}}{{t}_{1}}^{2}$ ………………….(ii)
${{s}_{2}}=u{{t}_{2}}+\dfrac{1}{2}{{a}_{2}}{{t}_{2}}^{2}$ ………….(iii)
Now, substituting the values in expression (ii) and (iii) we will get,
${{s}_{1}}=\left( 0 \right){{t}_{1}}+\dfrac{1}{2}\left( {{a}_{net}} \right){{t}_{1}}^{2}=\dfrac{1}{2}\left( a+g \right){{\left( 3 \right)}^{2}}$
$\Rightarrow {{s}_{1}}=\dfrac{1}{2}\left( 1+10 \right){{\left( 3 \right)}^{2}}=\dfrac{99}{2}=49.5\ meter$
${{s}_{2}}=\left( 0 \right){{t}_{2}}+\dfrac{1}{2}\left( {{a}_{net}} \right){{t}_{2}}^{2}=\dfrac{1}{2}\left( a+g \right){{\left( 1 \right)}^{2}}$
$\Rightarrow {{s}_{2}}=\dfrac{1}{2}\left( 1+10 \right){{\left( 1 \right)}^{2}}=\dfrac{11}{2}=5.5\ meter$
Now, the distance between stone 1 and 2 can be given by taking the difference of their distances which can be given as,
$s={{s}_{1}}-{{s}_{2}}=49.5-5.5=44\ meter$
Hence, the distance between two stones after 1 sec of being released is $44\ meters$.

Note: Student might forget to consider the initial velocity of the stones to be zero and might forget the principle i.e. if a body performs a free fall then initial velocity of the body is considered as zero and due to that they might make mistake in solving the problem so, students must take care while solving such problems.