Question

A balloon is ascending at the rate of $14m{s^{ - 1}}$ at a height of 98 above the ground when the food packet is dropped from the balloon. After how much time and with what velocity does it reach the ground? $Take\,g = \,9.8m{s^{ - 2}}$

Answer 1

Hint: By Equations of motion. Initial velocity of the packet is the same as that of the balloon as it lies inside the balloon and as it falls under gravity so the acceleration will be acceleration due to gravity and then by using equations of motion, it can be solved.

Complete step by step answer:
A balloon is ascending at the rate of $14\,m/s$ at a height of $98\,m$ above the ground.
Velocity of a Packet is in upward direction if we reverse its direction than its initial velocity is negative.

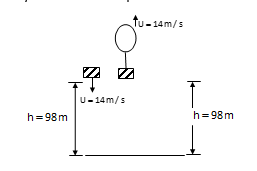
Hence
$U = - 14\,m/s$
$h = 98\,ms$
g (acceleration due to gravity) $ = 9.8\,m/{s^2}$
Use position velocity equation to find final velocity with which packet hit the ground
${V^2} - {U^2} = 2gh$ ……….(i)
Use given value in Equation (i)
${V^2} - {(14)^2} = 2(9.8)\,98$
${V^2} - 196\, = 1920.8$
${V^2} = 2116\,.8$
$V = \sqrt {2116.8} $
$v\, = 46\,m/s$ .
Now to find time after it will hit the ground use velocity time equation
$V = U + gt\,\,\,\,\,$ …………..(ii)
Use given values' in Equation (ii)
$46 = ( - 14) + 9.8\,\,t$
$46 + 14\,\, = 9.8\,t$
$t = \dfrac{{60}}{{9.8}} = 6.12\,seconds$

Note:To solve the above kind of questions use vector application Reverse the direction of velocity and make its value negative. So the negative sign here denotes the opposite direction only.