Question

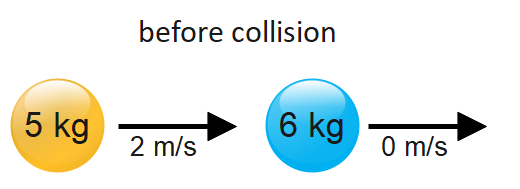
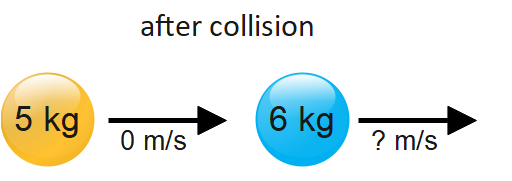
A ball with a mass of 5kg moving at 2 $m{s^{ - 1}}$ hits a still ball with a mass of 6kg. If the first ball stops moving, how fast is the second ball moving?

Answer 1

Hint: In order to solve the question, we will first take out the momentum before the collision of ball then we will take out the momentum after the collision which consist of the velocity of the second ball which we have to find then we will use the conservation of momentum to find the velocity.

Formula Used:
${\text{momentum = mass }} \times {\text{ velocity}}$
Law of conservation of momentum
${p_i} = {p_f}$
${p_i} = $initial momentum
${p_f} = $final momentum

Complete step by step solution:
In the question we are given that a moving ball hits another ball and the first ball stops moving and we have to find the how fast is the second ball is moving and we also have to find how much kinetic energy was lost as heat in the collision
Mass of ball 1st = 5 kg
Mass of ball 2nd = 6 kg
Velocity before collision of ball 1st = 2 $m{s^{ - 1}}$
Velocity before collision of ball 2nd = 0 $m{s^{ - 1}}$
Velocity after collision of ball 1st = 0 $m{s^{ - 1}}$
Velocity after collision of ball 2nd = $v_2$ $m{s^{ - 1}}$
In order to calculate the velocity of the second ball when it is hit by first ball, we will use the concept of conservation of momentum
Formula of momentum
${\text{momentum = mass }} \times {\text{ velocity}}$
Appling the momentum before collision

${p_i} = {m_1}{v_1} + {m_2}{v_2}$
Now we will substitute the mass of ball 1 and velocity of ball 1 before collision
${p_i} = 5kg \times 2m{s^{ - 1}} + 6kg \times 0m{s^{ - 1}}$
Therefore, momentum before collision is
${p_i} = 10{\text{ }}kg{\text{ }}m{s^{ - 1}}$
Appling the momentum after collision

${p_f} = {m_1}{v_1} + {m_2}{v_2}$
Now we will substitute the mass of ball 1 and velocity of ball 1 before collision
${p_f} = 5kg \times 0m{s^{ - 1}} + 6kg \times {v_2}$
${p_f} = 6kg \times {v_2}$
Now we use the law of conservation of momentum by equating initial momentum and final momentum
${p_i} = {p_f}$
Substituting the value of initial velocity and final velocity
$10{\text{ }}kg{\text{ }}m{s^{ - 1}} = 6kg \times {v_2}$
Now we will solve for velocity of ball 2 after collision
$${\text{ }}{v_2} = \dfrac{{10}}{6}m{s^{ - 1}}$$
Hence, the answer is $${\text{ }}{v_2} = \dfrac{{10}}{6}m{s^{ - 1}} = 1.6{\text{ }}m{s^{ - 1}}$$.

Note:
There might be a chance of making mistakes while equating the momentum. In the given case, both the balls are moving the same direction so we have equated them directly without any negative sign. Otherwise the equation depends on the direction of the velocity and according to that it is equated.