Question

A ball when dropped from a height of $200 m$ above ground level. At the same time a second ball is thrown from the ground in upward direction with an initial velocity of $80m/sec$. Then find time and the altitude of the ball when they cross each other?

Answer 1

Hint:We are given two balls moving in the opposite directions, we can assume they cross over height and time equal to a variable and then using the second equation of motion, we can find these values. The solution of these will give the required answer.

Complete step by step answer:
 A ball is dropped from a height of 200 m above ground level and at the same time a second ball is thrown from the ground in upward direction with an initial velocity of 80m/sec. the ball falling down will experience positive acceleration due to gravity while the one thrown upwards will experience retardation.

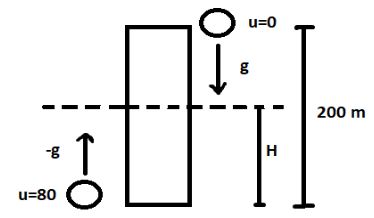
Let H and T be the height and T respectively where the two balls cross each.For the ball dropped from the top of the tower:
Distance covered by the ball is (200-H) m
Here
Initial velocity (u) = 0
Distance (S) = (200-H) m
Acceleration due to gravity (g) = $10m/{\sec ^2}$
To find the distance covered we can apply formula of motion in dimension as:
$S = ut + \dfrac{1}{2}g{t^2}$
Substituting the values, we get:
$200 - H = (o \times t) + \dfrac{1}{2}10{(T)^2}$
$\Rightarrow 200 - H = 5{T^2}$____(1)

Now for the ball thrown vertically upward:
Initial velocity (u) = 80 m/sec
Distance (S) = H = 200 m
Acceleration due to gravity (g) = $ - 10m/{\sec ^2}$
(Since experiencing retardation)
$S = ut - \dfrac{1}{2}g{t^2}$
Substituting the values, we get:
$H = \left( {80T} \right) - \dfrac{1}{2}10{T^2}$
$\Rightarrow H = 80T - 5{T^2}$_______(2)

Adding (1) and (2),we get
$200 - H + H = 5{T^2} + 80T - 5{T^2}$
$\Rightarrow T = 2.5\sec $
So in 2.5 seconds of time both ball will cross each other
Substituting value of T in equation (1)
We get $200 - H = 5{(2.5)^2}$
$\therefore H= 175\,m$

Thus, at 175m both balls will cross each other and after a time of 2.5 seconds they meet.

Note:When the body free falls, the only force experienced by the body is gravitational force and thus the acceleration experienced by the body is due to gravity represented by g. As g is always in the downward direction, the body falling downwards has positive g due to the same direction while the body thrown upwards has negative g because its motion is in the opposite direction to g.