Question

A ball thrown up in vacuum returns after 12 sec. Its position after five seconds will be same as after:
A. 7 sec
B. 3 sec
C. 4 sec
D. 3.5 sec

Answer 1

Hint: The time after which an object returns to the initial point is called time of flight. This time depends upon the velocity of projection, angle of projection and the acceleration due to gravity. The position of an object under uniformly accelerated motion can be determined by well-known equations.

Formula used:
$T_f = \dfrac{2u_y}{g}, v=u_y+at$

Complete answer:
Let’s first determine $u_y$ for the body.
Given $T_f = 12\ sec$
Hence using $T_f = \dfrac{2u_y}{g}$, we get
$12 = \dfrac{2u_y}{g}$
Or $u_y = 6g = 60\ m/s$
At t = 5 sec
The velocity of the object is given by $v=u-gt$
$v = 60 - 10\times5 = 10 m/s$

Concept:

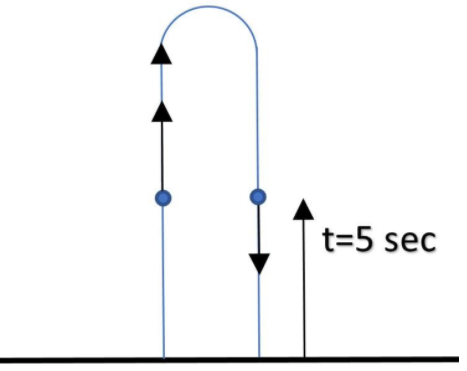
Now, in the question, it is asked to compute the time when the position is the same as position at 5 sec. This happens because the object will pass through the point first during going up and then coming back. But when it is coming back, the velocity will have the same magnitude but opposite direction. Thus using $v=u-gt$, here $v = -10m/s$ as per given condition.
Thus $-10 = 60 - 10 t$
Or $t=7\ sec$

Hence option A. is correct.

Note:
Since we require the time, we can also get it by solving for the position and then using $s=u_y t+\dfrac 12 gt^2$ and solving for quadratic, we’ll get two values of ‘t’ which denotes that the body will pass through the same position, twice. In the solution, we’ve used the y – component of velocity ($u_y$). This is only because this concept is also true if the body is not projected vertically upwards. It is also true for parabolic trajectory either. But in that case, we’ll use the y component of initial velocity as only y component is responsible for the time x- component is only responsible for travelling of the body along x axis.