
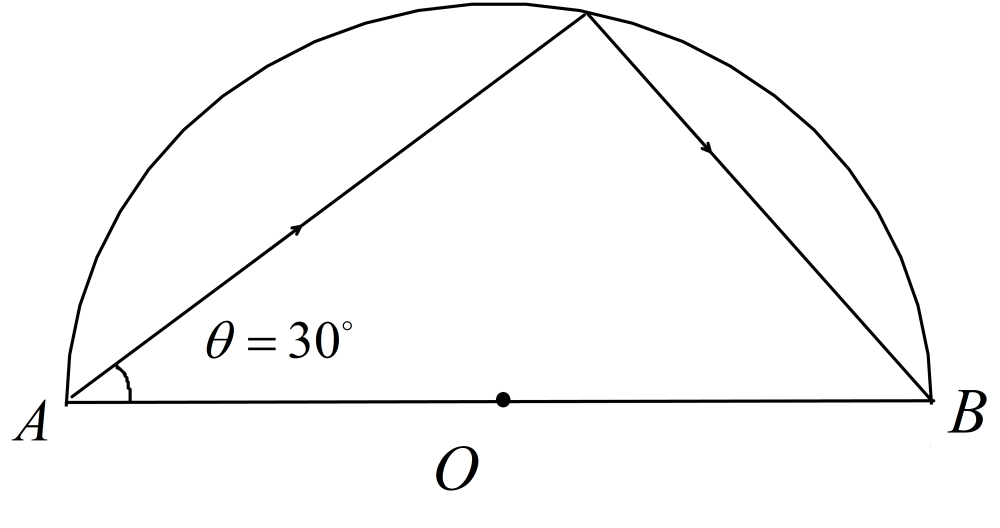
A ball thrown from position A against a smooth circular wall rebounds and hits position B at the other end of the diameter through A. If the coefficient of restitution between wall and ball is $ e $ and $ \theta = {30^ \circ } $ , then find $ 3e $ . Do not consider any force on the ball except contact force due to the wall at the time of the collision.
(A) $ 1 $
(B) $ \dfrac{1}{4} $
(C) $ \dfrac{1}{5} $
(D) $ \sqrt 3 $

Answer
516.3k+ views
Hint: It is known that the coefficient of restitution is defined as the ratio of the final to initial relative velocity between two objects after they collide. Expression for the coefficient of restitution for a body colliding with an rigid body at rest is given by, $ e = \dfrac{{{v_{normal}}}}{{{u_{normal}}}} $ where, $ {v_{normal}} $ is the component of the final velocity normal with the impact surface and $ {u_{normal}} $ is the component of the initial velocity normal with the impact surface.
Complete step by step solution:
We know that the coefficient of restitution is defined as the ratio of the final to initial relative velocity between two objects after they collide.
Expression for the coefficient of restitution for a body colliding with an rigid body at rest is given by, $ e = \dfrac{{{v_{normal}}}}{{{u_{normal}}}} $ where, $ {v_{normal}} $ is the component of the final velocity normal with the impact surface and $ {u_{normal}} $ is the component of the initial velocity normal with the impact surface.
Now, here we have a circular wall as an impact surface. So, the normal component of velocity will be along the normal of the circle.
Now, let's say the initial velocity of the ball is $ u $ and final velocity of the ball is $ v $ .
From the figure we can see that the normal component (along $ OD $ ) of initial velocity is the same as the horizontal component of the initial velocity (along $ AB $ ), since the $ \Delta AOB $ is an isosceles triangle. So, we can take the normal (along $ OD $ ) and tangential(along the tangent of the circle) component of velocity as mutually orthogonal components as in the polar coordinate system.
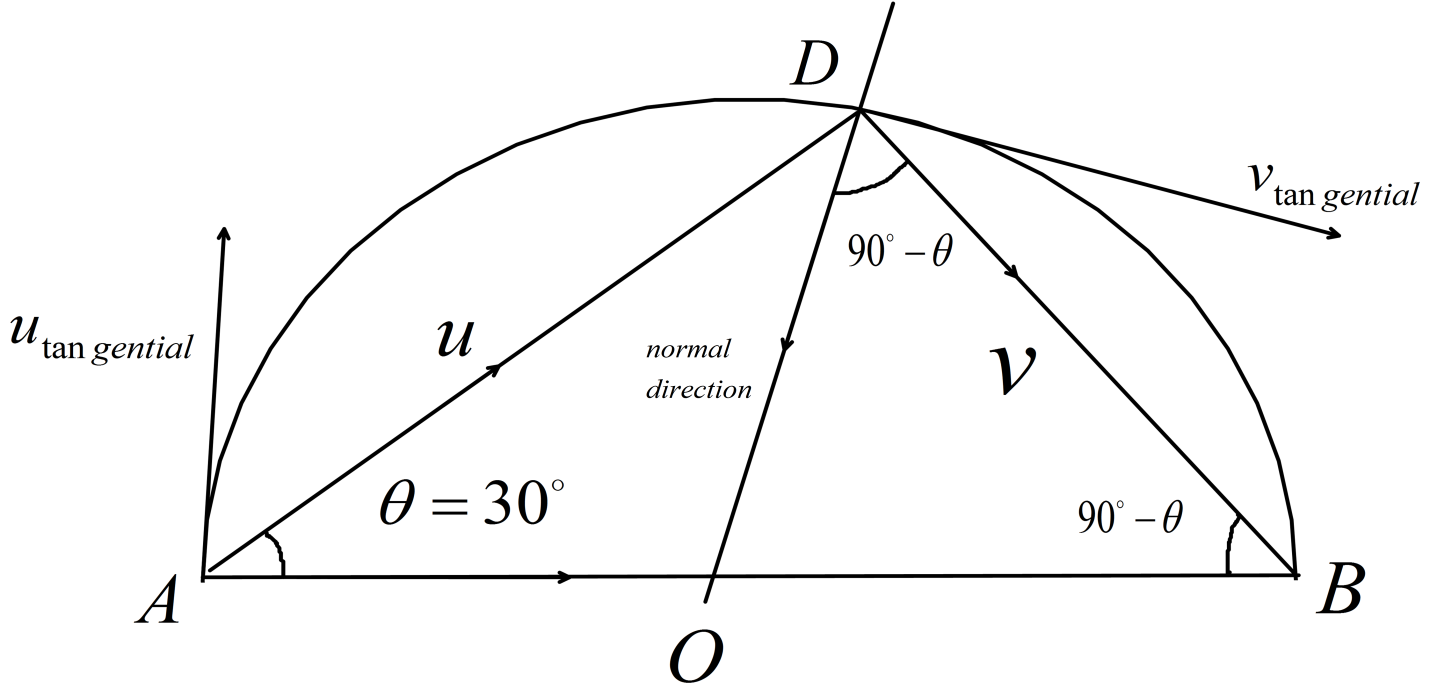
So, we can write, $ {u_{normal}} = u\cos \theta $ and $ {u_{tangential}} = u\sin \theta $
For, final velocity $ {v_{normal}} = v\sin \theta $ and $ {v_{tangential}} = v\cos \theta $ .
So, the coefficient of restitution becomes, $ e = \dfrac{{{v_{normal}}}}{{{u_{normal}}}} = \dfrac{{ - v\sin \theta }}{{u\cos \theta }} $ [ Since, they are in opposite direction.]
Simplifying we get, $ eu\cos \theta = - v\sin \theta $
Since, we know the horizontal component of the velocity does not change due to collision so we can write, $ {u_{tangential}} = {v_{tangential}} $
Or, $ u\sin \theta = v\cos \theta $ .
taking only magnitude and rewriting the equations we get,
$ eu\cos \theta = v\sin \theta $
and, $ u\sin \theta = v\cos \theta $ .
Dividing the equations we get,
$ e\cot \theta = \tan \theta $
Or, $ e = {\tan ^2}\theta $
Here, given $ \theta = {30^ \circ } $ . Putting the value we get,
$ e = {\left( {\dfrac{1}{{\sqrt 3 }}} \right)^2} = \dfrac{1}{3} $
Or, $ 3e = 1 $
Hence, the magnitude of $ 3e $ is $ 1 $. So, option (A ) is correct.
Note:
$ \bullet $ The tangential component of the velocity is always acting tangentially though the magnitude of the initial and final velocity is different along the tangential direction in the Cartesian system but they are always equivalent in the polar coordinate system. If the collision happened with a smooth perpendicular wall then one has to use the components in the Cartesian coordinate system.
$ \bullet $ Collision of an object with body at rest is always two dimensional
Complete step by step solution:
We know that the coefficient of restitution is defined as the ratio of the final to initial relative velocity between two objects after they collide.
Expression for the coefficient of restitution for a body colliding with an rigid body at rest is given by, $ e = \dfrac{{{v_{normal}}}}{{{u_{normal}}}} $ where, $ {v_{normal}} $ is the component of the final velocity normal with the impact surface and $ {u_{normal}} $ is the component of the initial velocity normal with the impact surface.
Now, here we have a circular wall as an impact surface. So, the normal component of velocity will be along the normal of the circle.
Now, let's say the initial velocity of the ball is $ u $ and final velocity of the ball is $ v $ .
From the figure we can see that the normal component (along $ OD $ ) of initial velocity is the same as the horizontal component of the initial velocity (along $ AB $ ), since the $ \Delta AOB $ is an isosceles triangle. So, we can take the normal (along $ OD $ ) and tangential(along the tangent of the circle) component of velocity as mutually orthogonal components as in the polar coordinate system.

So, we can write, $ {u_{normal}} = u\cos \theta $ and $ {u_{tangential}} = u\sin \theta $
For, final velocity $ {v_{normal}} = v\sin \theta $ and $ {v_{tangential}} = v\cos \theta $ .
So, the coefficient of restitution becomes, $ e = \dfrac{{{v_{normal}}}}{{{u_{normal}}}} = \dfrac{{ - v\sin \theta }}{{u\cos \theta }} $ [ Since, they are in opposite direction.]
Simplifying we get, $ eu\cos \theta = - v\sin \theta $
Since, we know the horizontal component of the velocity does not change due to collision so we can write, $ {u_{tangential}} = {v_{tangential}} $
Or, $ u\sin \theta = v\cos \theta $ .
taking only magnitude and rewriting the equations we get,
$ eu\cos \theta = v\sin \theta $
and, $ u\sin \theta = v\cos \theta $ .
Dividing the equations we get,
$ e\cot \theta = \tan \theta $
Or, $ e = {\tan ^2}\theta $
Here, given $ \theta = {30^ \circ } $ . Putting the value we get,
$ e = {\left( {\dfrac{1}{{\sqrt 3 }}} \right)^2} = \dfrac{1}{3} $
Or, $ 3e = 1 $
Hence, the magnitude of $ 3e $ is $ 1 $. So, option (A ) is correct.
Note:
$ \bullet $ The tangential component of the velocity is always acting tangentially though the magnitude of the initial and final velocity is different along the tangential direction in the Cartesian system but they are always equivalent in the polar coordinate system. If the collision happened with a smooth perpendicular wall then one has to use the components in the Cartesian coordinate system.
$ \bullet $ Collision of an object with body at rest is always two dimensional
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Class 11 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Trending doubts
10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Explain zero factorial class 11 maths CBSE

What is a periderm How does periderm formation take class 11 biology CBSE




