Question

A ball starts falling with zero initial velocity on a smooth inclined plane forming an angle \[\alpha \] with the horizontal. Having fallen the distance h, the ball rebounds elastically off the inclined plane. At a distance \[l=xhsin\alpha \] from the impact point the ball rebounds for the second time. Find \[x\].

Answer 1

Hint:
To find the value of the \x\in terms of height, gravity and angular acceleration, we first need to find the displacement of the ball in both X and a Y direction from origin to the next point on the inclined plane the ball drops. The acceleration will be taken in terms of angular acceleration and gravity. The formulas for the distance between the two ball drops are:
\[{{D}_{x,y}}={{u}_{x,y}}t+\dfrac{1}{2}{{a}_{x,y}}{{t}^{2}}\]
\[{{D}_{x,y}}\] is the displacement in both X and Y direction separately, \[{{u}_{x,y}}\] is the velocity of the ball in both X and Y direction, \[{{a}_{x,y}}\] is the angular acceleration of the ball in terms of gravity and angular acceleration in both X and Y direction and \[t\] is the time taken for the ball from origin to the next drop.

Complete step by step solution:
According to the question, a diagram is drawn showing the motion of the ball as it is dropped on the inclined plane.

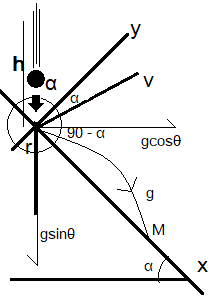
The ball falls with zero initial velocity meaning the velocity achieved when the ball hits the surface of the inclined plane the velocity becomes final velocity of \[v=\sqrt{2gh}\].
After the ball hits the tip of the inclined surface, the ball jumps downward on the inclined surface at point M from an angle of \[90-\alpha \], the velocity of the release of the ball from origin to M is the same as the final velocity at the top when the ball hits the surface i.e. \[v=\sqrt{2gh}\].
Now, the distance from the origin to the point P can be calculated on the basis final and initial velocity along with the time taken when the ball was in mid-air in both X and Y axis direction.
For Y-direction, the displacement of the ball is:
\[{{D}_{y}}={{u}_{y}}t+\dfrac{1}{2}{{a}_{y}}{{t}^{2}}\]
Placing the values of the acceleration \[a\] as \[a=g\cos \alpha \] for horizontal direction as shown in the diagram and the velocity as \[u\cos \alpha \] and the displacement is zero as the ball doesn’t go horizontal. Hence, the time calculated is:
\[0=u\cos \alpha \left( \dfrac{2{{u}_{o}}}{g} \right)+\dfrac{1}{2}g\cos \alpha {{\left( \dfrac{2{{u}_{o}}}{g} \right)}^{2}}\]
\[\Rightarrow u\cos \alpha \left( \dfrac{2{{u}_{o}}}{g} \right)=-\dfrac{1}{2}g\cos \alpha {{\left( \dfrac{2{{u}_{o}}}{g} \right)}^{2}}\]
\[\Rightarrow u=-\dfrac{1}{2}g\left( \dfrac{2{{u}_{o}}}{g} \right)t\]
\[\Rightarrow t=\dfrac{2u}{g}\]
For X-direction, the displacement of the ball is:
\[{{D}_{x}}={{u}_{x}}t+\dfrac{1}{2}{{a}_{x}}{{t}^{2}}\]
Placing the values of the acceleration \[a\] as \[a=g\sin \alpha \] for vertical direction downward as shown in the diagram and \[t\] as \[t=\dfrac{2u}{g}\] and the velocity as \[u\sin \alpha \] and the displacement as \[l\].
\[l=u\sin \alpha \left( \dfrac{2{{u}_{o}}}{g} \right)+\dfrac{1}{2}g\sin \alpha {{\left( \dfrac{2{{u}_{o}}}{g} \right)}^{2}}\]
\[\Rightarrow \dfrac{4{{u}^{2}}\sin \alpha }{g}\]
Placing the velocity in terms of gravity and distance from the height ball was dropped as \[{{u}^{2}}=2gh\]. The length as given in the question is \[l=xhsin\alpha \] and the distance obtained is:
\[l=\dfrac{4{{u}^{2}}\sin \alpha }{g}\]
\[\Rightarrow \dfrac{4\times 2\times g\times h\sin \alpha }{g}\]
Therefore, the value of length is \[l=8h\sin \alpha \] and after matching with \[l=xhsin\alpha \], we get the value of \[x=8\].

Note: When the ball falls on the inclined surface, there are two directions on which the ball’s fall is dependent: the X direction and Y direction, the velocity and acceleration both have the X and Y direction. Now students may go wrong when they try to plot the distance as the distance length \[l\] is for the X direction and not for the Y direction, the same goes for acceleration and velocity as well.