Question

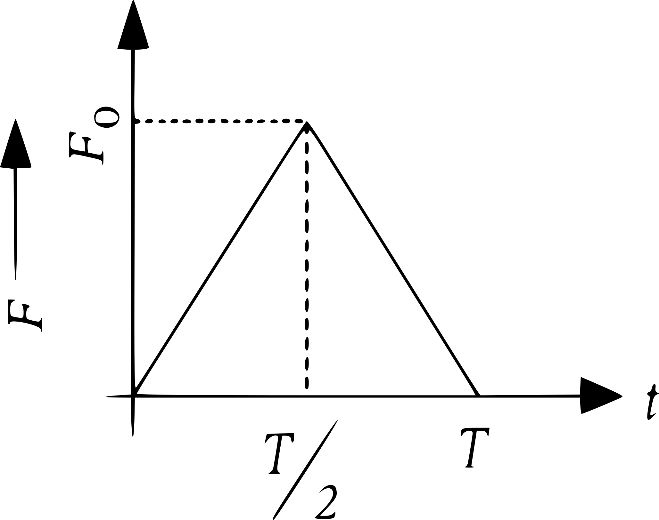
A ball of mass m moving with a velocity v rebounds from a wall. The collision is assumed elastic and the force of interaction between the ball and wall varies as shown is the figure. Then, the value of ${{F}_{0}}$ is:

Answer 1

Hint: We know that momentum is a physics term it refers to the quantity of motion that an object has. A sports team that is on the move has the momentum. If an object is in motion (on the move) then it has momentum. One example is the use of air bags in automobiles. Air bags are used in automobiles because they are able to minimize the effect of the force on an object involved in a collision. Air bags accomplish this by extending the time required to stop the momentum of the driver and passenger. Momentum is mass in motion, and any moving object can have momentum. An object's change in momentum is equal to its impulse. Impulse is a quantity of force times the time interval. Impulse is not equal to momentum itself; rather, it's the increase or decrease of an object's momentum. Based on this concept we have to solve this question.

Complete step by step answer
The diagram of the question is given below:

We know that area under force-time graph gives change in linear momentum
So now the area is given as:
area $=\dfrac{1}{2} \mathrm{F}_{\mathrm{o}} \mathrm{T}=$ change in linear momentum
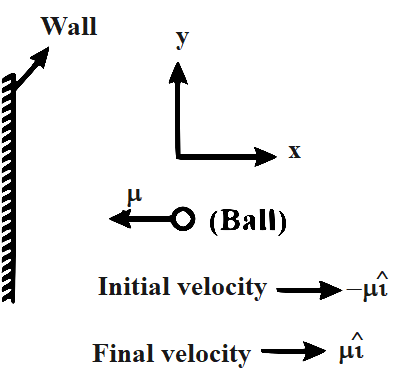
So, we can say that $\mathrm{v}_{1}=-\mathrm{u},$ negative sign represents initial velocity is in negative $\mathrm{x}-$direction according to our sign convention.
Now again we can write that:
$\mathrm{v}_{2}=\mathrm{u},$ final velocity is in positive $\mathrm{x}$ - direction
Now we have to find the momentum:
The initial momentum is given as:
initial momentum $=\mathrm{m}(-\mathrm{u})=-\mathrm{mu}$
The final momentum is given as:
final momentum= \[mu\]
Now the change in linear momentum:
change in linear momentum= $2 \mathrm{mu}$
So, the expression is given as:
$\dfrac{1}{2} \mathrm{F}_{\mathrm{o}} \mathrm{T}=2 \mathrm{mu}$
Now the answer is given as:
$\Rightarrow {{\text{F}}_{\text{o}}}=\dfrac{4\text{mu}}{\text{T}}$

Note: We should know that linear momentum is defined as the product of a system's mass multiplied by its velocity. In symbols, linear momentum is expressed as $p\text{ }=\text{ }mv$. Momentum is directly proportional to the object's mass and also its velocity. Thus, the greater an object's mass or the greater its velocity, the greater its momentum. Note that the linear moment is a vector quantity and is conserved in any direction. In the center-of-mass system, the total momentum is always zero, before and after the interaction, in any direction. Angular momentum is inertia of rotation motion. Linear momentum is inertia of translation motion. The big difference is that the type of motion which is related to each momentum is different. It is important to consider the place where the force related to rotation applies, which appears as 'r' in the formula.