Question

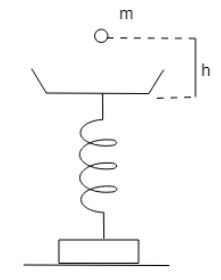
A ball of mass $m$ is dropped from a height h on a platform fixed at the top of a vertical spring. The platform is displaced by a distance $x$. The spring constant is (Take acceleration due to gravity $ = g$):

A. $\dfrac{{2mg}}{x}$
B. \[\dfrac{{2mgh}}{{{x^2}}}\]
C. \[\dfrac{{2mg(h + x)}}{{{x^2}}}\]
D. \[\dfrac{{2mg(h + x)}}{{{h^2}}}\]

Answer 1

Hint: In this question, we will apply the law of conservation of energy. First we will find the loss in the gravitational potential energy of the particle and then we will find the elastic potential energy. On equating these two equations, we will get the final answer.

Complete step by step answer:
We know that the law of conservation of energy says that any form of energy which is present in this universe can neither be created nor be destroyed. So, we can say that the energy in this universe always remains conserved but the transformation of energy from one state to another state can easily take place.

In this question, the gravitational potential energy of the particle which is lost when the particle falls is equally converted into the elastic potential energy of the spring. So, we can say that the transformation of gravitational potential energy to elastic potential energy is taking place.So,
Loss in gravitational potential energy = gain in elastic potential energy of this spring
Loss in gravitational potential energy \[ = mg(h + x).......(1)\]
$(h + x)$ is the loss of height in which $h$ is the height from which the particle falls and $x$ is the displacement in the platform.

Gain in the elastic potential energy of the spring $ = \dfrac{1}{2}k{x^2}.....(2)$
Where, $k$ is the spring constant and $x$ is the displacement in the platform.
On equating equation (1) and equation (2), we get,
$mg(h + x) = \dfrac{1}{2}k{x^2}$
On keeping spring constant on one side and taking all the other terms on the other side, we get,
$\therefore k = \dfrac{{2mg(h + x)}}{{{x^2}}}$

Therefore, the correct answer is C.

Note: The definition of spring constant is that it is the force needed to stretch or compress a spring divided by the distance by which the spring gets longer or shorter. The function of the spring constant is to find out the stability or instability present in a spring.