Question

A ball of mass m hits a wall with a speed v making an angle$\theta $ with the normal. If the coefficient of restitution is e, the direction and magnitude of the velocity of ball after reflection from the wall will respectively be:
A) ${\tan ^{ - 1}}\left( {\dfrac{{\tan \theta }}{e}} \right),\left( {\sqrt {{{\sin }^2}\theta + {{\cos }^2}\theta } } \right)v$
B) ${\tan ^{ - 1}}\left( {\dfrac{e}{{\tan \theta }}} \right),\left( {\dfrac{1}{v}\sqrt {{e^2}{{\sin }^2}\theta + {{\cos }^2}\theta } } \right)v$
C) ${\tan ^{ - 1}}\left( {e\tan \theta } \right),\dfrac{v}{e}\tan \theta $
D) ${\tan ^{ - 1}}\left( {e\tan \theta } \right),v\sqrt {\sin \theta + {e^2}} $

Answer 1

Hint:In order to find the solution we will follow the rule of angle of reflection which states that the angle of incidence is equal to angle of reflection and hence we will prove that$\theta = \theta '$. The given condition is elastic in nature and hence the coefficient of restitution e will be equal to 1 which will eventually tell us the velocities before and after collision is the same.

Step by step solution:
Step 1:
We are given:
A ball of mass m hits a wall with a speed v making an angle$\theta $ with the normal
The coefficient of restitution is e
Here we have a diagram to represent the various quantities.

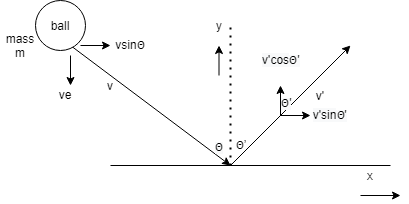
The ball is hitting the wall with the speed of v and reflected by the velocity v’. It makes an angle of $\theta $ when hitting and then reflected by an angle of$\theta '$
The momentum will be conserved because no external force is being applied on the system before and after the hitting
This implies the momentum will be conserved in both x and y direction
The ball before and after hitting is moving along the x-direction and hence it is proceeding toward the sine component
The conservation of momentum for x will be $mv\sin \theta $ =$mg'\sin \theta '$ ……. (1)
From equation 1 we can say that $v\sin \theta = v'\sin \theta '$ …… (2)
The coefficient of restitution e is defined as divide of velocity of separation divide by velocity of approach, e=$\dfrac{{{v_{separation}}}}{{{v_{approach}}}}$ and from the diagram we can say that velocity of approach is $v\cos \theta $ and velocity of separation is$v'\cos \theta '$
So rewriting coefficient of restitution e=$\dfrac{{v'\cos \theta '}}{{v\cos \theta }}$ $ \Rightarrow v'\cos \theta ' = ev\cos \theta $ …….. (3)
Now squaring the equation 2 and 3 and adding them we get,${\left( {v'} \right)^2} = {v^2}({\sin ^2}\theta + {e^2}{\cos ^2}\theta )$
Taking root both sides we get,$v' = \sqrt {{{\sin }^2}\theta + {e^2}{{\cos }^2}\theta } v$ …… (4)
In elastic collision the coefficient of restitution e is equal to 1 and also the trigonometric identity says${\sin ^2}\theta + {\cos ^2}\theta = 1$. Putting it in equation 4 we get, $v' = v$
Now dividing equation from equation 3, we get: $\tan \theta ' = \dfrac{1}{e}\tan \theta $….. (5)
As we have said that it is elastic collision so coefficient of restitution will be 1 then$\theta ' = \theta $
Angle of incidence is equal to angle of reflection.

Hence, from equation 4 and 5 our correct option is A.

Note:There is a rule of separating two vectors from the component. When we separate them then the side which is closer to the angle made by them will be called as $\cos \theta $ and the angle made by it far from the component will be called as $\sin \theta $ as shown in the figure above. They are perpendicular to each other.