Question

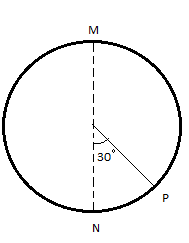
A ball of mass $\dfrac{1}{2}$ kg is moved in a vertical circle. When the ball is at P, then calculate its tangential acceleration. [ take, $g = 10m/{s^2}$ ]

$(1)\;{\text{2 m/}}{{\text{s}}^2}$
$(2)\;3{\text{ m/}}{{\text{s}}^2}$
$(3)\;5{\text{ m/}}{{\text{s}}^2}$
$(4)\;1{\text{ m/}}{{\text{s}}^2}$

Answer 1

Hint: Here we will frame the equation to find the tangential equation using the correlation between the formula of the force and the weight of an object. Place the values in the derived equation and simplify for the resultant answer.

Complete step by step answer:
Given that the ball makes an angle $ = 30^\circ $ with the vertical at point P.
So, the component of weight along the tangent is $W = mg\sin 30^\circ $
At equilibrium, the weight of an object is equal to the force of the object.
$ \Rightarrow F = mg\sin 30^\circ $
We also know that force of an object is the product of the object and the acceleration faced by the object.
$ \Rightarrow ma = mg\sin 30^\circ $
Same terms from both sides of the equation cancel each other. Therefore remove “m” mass from both the sides of the equation.
$ \Rightarrow a = g\sin 30^\circ $
Place the known values in the above equation – $\sin 30^\circ = \dfrac{1}{2}$
$ \Rightarrow a = 10 \times \dfrac{1}{2}$
Simplify the above equation –
$ \Rightarrow a = 5m/{s^2}$
Therefore, the tangential acceleration of the ball is $5m/{s^2}$

So, the correct answer is “Option 3”.

Note:
Know the correct formula to find the tangential acceleration, place the values and simplify the equations using basic properties then rest goes well. Please remember all the different trigonometric angles given by the ratios of the trigonometric functions. The most important trigonometric angles are $0^\circ ,{\text{ 3}}0^\circ ,\;45^\circ ,{\text{ 6}}0^\circ {\text{ and 9}}0^\circ $. Remember the values of these angles for quick substitution for further accurate and efficient simplification.