Question

A ball of mass $ 160g $ is thrown up at an angle of $ {60^ \circ } $ to the horizontal at a speed of $ 10m{s^{ - 1}} $ . The angular momentum of the ball at the highest point of its trajectory with respect to the point from which the ball is thrown is nearly: $ \left( {g = 10m{s^{ - 2}}} \right) $
(A) $ 1.73kg{m^2}/s $
(B) $ 3.0kg{m^2}/s $
(C) $ 3.46kg{m^2}/s $
(D) $ 6.0kg{m^2}/s $

Answer 1

Hint To solve this question, we need to use the basic formula of the angular momentum. The initial conditions of the projectile motion will give the values of the necessary parameters required for obtaining the final answer.

Formula Used: The formula used in solving this question is given by
 $\Rightarrow \vec L = m\left( {\vec v \times \vec r} \right) $ , where $ L $ is the angular momentum of an object whose mass is $ m $ , velocity is $ v $ and the position vector is $ r $

Complete step by step answer
We know that the angular momentum is given by the expression
 $\Rightarrow \vec L = m\left( {\vec v \times \vec r} \right) $ $ \vec L = m\left( {\vec v \times \vec r} \right) $
Writing the above equation in terms of the magnitude, we get
 $\Rightarrow L = mvr\sin \varphi $ …………………….(i)
Where $ \varphi $ is the angle between the velocity and the position vector of the object.
Now, since we have to find the angular momentum with respect to the starting point, we take the origin there. The motion of the ball is shown in the figure below.

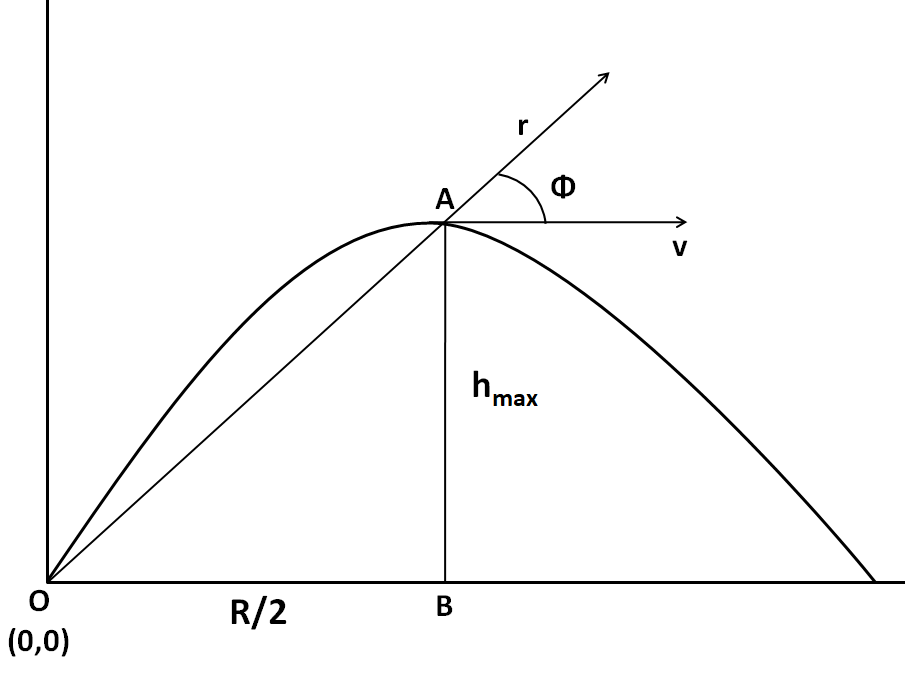
As we know that at the highest point, the velocity vector becomes parallel to the horizontal, so the velocity at A is
 $\Rightarrow v = u\cos \theta $
According to the question, $ \theta = {60^ \circ } $
 $\Rightarrow v = \dfrac{u}{2} $ …………………….(ii)
Since point A is at the highest point, the height of the ball at A is given by
 $\Rightarrow AB = {h_{\max }} = \dfrac{{{u^2}{{\sin }^2}\theta }}{{2g}} $ …………………….(ii)
The horizontal distance covered by the ball at A is equal to half the maximum range of the ball, which is
 $\Rightarrow OB = \dfrac{R}{2} = \dfrac{{{u^2}\sin 2\theta }}{{2g}} $ …………………….(iv)
Now, in triangle OAB, by the Pythagoras Theorem
 $\Rightarrow O{A^2} = A{B^2} + O{B^2} $
 $\Rightarrow {r^2} = {h_{\max }}^2 + {\left( {\dfrac{R}{2}} \right)^2} $
From (ii) and (iii)
 $\Rightarrow {r^2} = {\left( {\dfrac{{{u^2}{{\sin }^2}\theta }}{{2g}}} \right)^2} + {\left( {\dfrac{{{u^2}\sin 2\theta }}{{2g}}} \right)^2} $
 $\Rightarrow {r^2} = {\left( {\dfrac{{{u^2}}}{{2g}}} \right)^2}\left( {{{\sin }^4}\theta + {{\sin }^2}2\theta } \right) $
We know that $ \sin 2\theta = 2\sin \theta \cos \theta $ . Making this substitution above, we get
 $\Rightarrow {r^2} = {\left( {\dfrac{{{u^2}}}{{2g}}} \right)^2}\left( {{{\sin }^4}\theta + 4{{\sin }^2}\theta {{\cos }^2}\theta } \right) $
Taking square root both sides
 $\Rightarrow r = \dfrac{{{u^2}}}{{2g}}\sqrt {\left( {{{\sin }^4}\theta + 4{{\sin }^2}\theta {{\cos }^2}\theta } \right)} $
According to the question, $ \theta = {60^ \circ } $ . Therefore
 $\Rightarrow r = \dfrac{{{u^2}}}{{2g}}\sqrt {\left( {{{\left( {\dfrac{{\sqrt 3 }}{2}} \right)}^4} + 4{{\left( {\dfrac{{\sqrt 3 }}{2}} \right)}^2}{{\left( {\dfrac{1}{2}} \right)}^2}} \right)} $
 $\Rightarrow r = \dfrac{{{u^2}}}{{8g}}\sqrt {21} $ …………………….(v)
Also, $ \tan \varphi = \dfrac{{AB}}{{OB}} $
Putting (ii) and (iii)
 $\Rightarrow \tan \varphi = \dfrac{{\dfrac{{{u^2}{{\sin }^2}\theta }}{{2g}}}}{{\dfrac{{{u^2}\sin 2\theta }}{{2g}}}} $
 $\Rightarrow \tan \varphi = \dfrac{{{{\sin }^2}\theta }}{{\sin 2\theta }} $
Substituting $ \sin 2\theta = 2\sin \theta \cos \theta $
 $\Rightarrow \tan \varphi = \dfrac{{{{\sin }^2}\theta }}{{2\sin \theta \cos \theta }} $
 $\Rightarrow \tan \varphi = \dfrac{{\tan \theta }}{2} $
According to the question, $ \theta = {60^ \circ } $ . Therefore
 $\Rightarrow \tan \varphi = \dfrac{{\sqrt 3 }}{2} $
From here, it is easy to show that
 $\Rightarrow \sin \varphi = \sqrt {\dfrac{3}{7}} $ …………………….(vi)
Now, from (i) we have
 $\Rightarrow L = mvr\sin \varphi $
Putting (iv), (v) and (vi)
 $\Rightarrow L = m\dfrac{u}{2}\left( {\dfrac{{{u^2}}}{{8g}}} \right)\sqrt {21} \sqrt {\dfrac{3}{7}} $
 $\Rightarrow L = \dfrac{{3m{u^3}}}{{16g}} $
According to the question
 $\Rightarrow m = 160g = 0.16kg $
 $\Rightarrow u = 10m{s^{ - 1}} $
 $\Rightarrow L = \dfrac{{3\left( {0.16} \right){{\left( {10} \right)}^3}}}{{160}} $
Finally on solving we get
 $\Rightarrow L = 3kg{m^2}{s^{ - 1}} $
Hence, the correct answer is option B.

Note
Do not get confused between the initial angle of projection and the angle between the position vector and the velocity. They are different, do not make them equal. For avoiding this confusion we have denoted the latter by the Greek letter $ \varphi $ .