Question

A ball of mass $100$g is projected vertically upward from the ground with a velocity of $49$m/s. At the same time another ball is dropped from a height of $98$m to fall freely along the same path as the first ball. After some time the two balls collide and stick together and finally fall together. Find the time of flight of masses.
A. $3.2$s
B. $12.6$s
C. $7.5$s
D. $6.5$s

Answer 1

Hint: By using the equations of motion for both balls, time of flight can be calculated. As other ball is falling freely, so its initial velocity will be zero

Complete step by step answer:
Let the two balls be A and B as both balls are identical, so mass
Of both will be same i.e.
${m_A} = {m_B} = 100g$

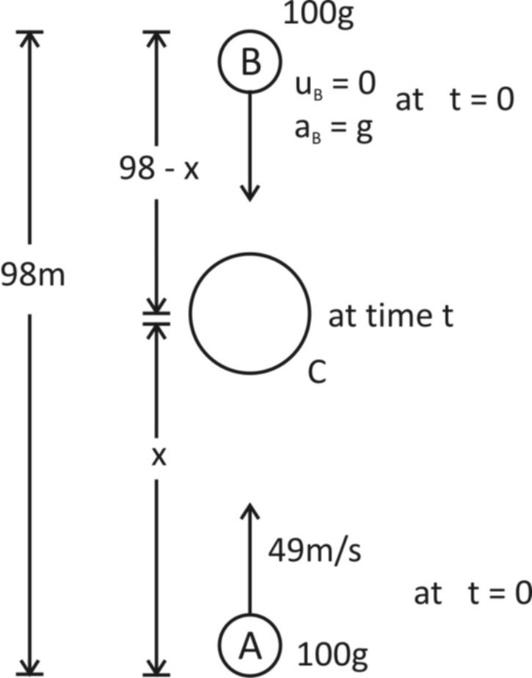
Where ${m_A}$ denotes mass of A ball and ${m_B}$ is mass of ball B.
Now, initially
For ball B, it moves freely downward so, initial velocity of B, ${u_B} = 0$
Acceleration, $a = g = 9.8m/{s^2}$
Let both collide at C. after time t so, distance, $s = \left( {98 - x} \right)m$
Now, $S = ut + \dfrac{1}{2}a{t^2}$
$98 - x = 0t + \dfrac{1}{2} \times g \times {t^2}$
$98 - x = \dfrac{1}{2} \times 9.8 \times {t^2}$
$x = 98 - 4.9{t^2}$… (i)
Initial velocity, ${u_A} = 49m/s$
Acceleration, $a = - g = - 9.8m/{s^2}$
And $s = x$
So, $s = ut + \dfrac{1}{2}a{t^2}$
$x = 49t + \dfrac{1}{2}\left( { - g} \right){t^2}$
$x = 49t - \dfrac{{9.8}}{2}{t^2}$
$ \Rightarrow x = 49t - 4.9{t^2}$… (ii)
From (i) and (ii)
$49t - 4.9{t^2} = 98 - 4.9{t^2}$
$49t = 98$
$t = 98/49 = 2$
$t = 2\sec $
And $x = 98 - 4.9{\left( 2 \right)^2} = 98 - 19.6$
$ = 78.4m$
After $2$sec, velocity of A in upward direction, ${V_A} = {u_A} - gt = 49 - 9.8 \times 2$
${V_A} = 29.4m/s$
And velocity of B in downward direction after $2$sec, ${V_B} = 9.8 \times 2 = 19.6m/s$
So, net upward momentum $ = p = m \times 29.4 - m \times 19.6$
$ = 4.8m$
Net upward momentum of combined mass
$P = 2m\left( v \right)$
Where v is final velocity,
By conservation of mass,
$2m\left( v \right) = 9.8m$
$\left( v \right) = \dfrac{{9.8m}}{{2m}} = \dfrac{{9.8}}{2} = 4.9m/s$
Height from ground, $x = 78.4m$
So, $S = ut + \dfrac{1}{2}a{t^2}$
$
   \Rightarrow x = - V\left( t \right) + \dfrac{1}{2}g{t^2} \\
   \Rightarrow 78.4 = - 4.9t - \dfrac{{9.8}}{2}{t^2} \\
   \Rightarrow t = 4.5\sec \\
 $
So, total time of flight, $T = 4.5 + 2$
$ = 6.5\sec $

So, the correct answer is “Option D”.

Note:
Total time of flight is the sum of time after which collision occurs and time at which body returns its ground after collision.Also remember that here the mass of A is equal to mass of B.