Question

A ball of mass 1 kg is released from position A inside a fixed wedge with a hemispherical cut of radius 0.5 m as shown in the figure. Find the force exerted by the vertical wall OM on wedge, when the ball is in position B. (Neglect friction everywhere). (Take \[g = 10\,{\text{m/}}{{\text{s}}^2}\])

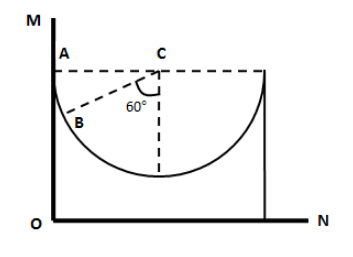
Answer 1

Hint:At the position B, the ball will exert a force on the wall OM due to the centrifugal force acting on the ball. To determine the centrifugal force, we have to determine the velocity of the ball at position B. To do so, use the law of conservation of energy. Only the horizontal component of the centrifugal force will exert the force on the wall OM.

Formula used:
Kinetic energy, \[K = \dfrac{1}{2}m{v^2}\], where, m is the mass and v is the velocity.
Potential energy, \[P = mgh\], where, g is the acceleration due to gravity and h is the height.
Centrifugal force, \[{F_C} = \dfrac{{m{v^2}}}{R}\], here, R is the radius of circular motion.

Complete step by step answer:
At the position B, the ball will exert a force on the wall OM due to the centrifugal force acting on the ball. To determine the centrifugal force, we have to determine the velocity of the ball at position B. To do so, we can use the law of conservation of energy. The kinetic energy obtained by the ball at position B is equal to potential energy lost by the ball. Therefore, we can write,
\[\dfrac{1}{2}m{v^2} = mgh\]
\[ \Rightarrow v = \sqrt {2gh} \] …… (1)

Now, we have to determine the vertical distance between position A and B. Let’s draw the free body diagram of the forces acting on the ball at position B as shown in the figure below.

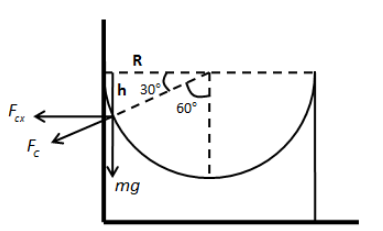
From the geometry of the above figure, we can write,
\[\tan 30^\circ = \dfrac{h}{R}\]
\[ \Rightarrow h = R\tan 30^\circ \]
\[ \Rightarrow h = \dfrac{R}{{\sqrt 3 }}\]
Substituting \[h = \dfrac{R}{{\sqrt 3 }}\] in equation (1), we get,
\[v = \sqrt {\dfrac{{2gR}}{{\sqrt 3 }}} \] …… (2)
We know the centrifugal force is given as,
\[{F_C} = \dfrac{{m{v^2}}}{R}\]
Substituting equation (2) in the above equation, we get,
\[{F_C} = \dfrac{m}{R}\dfrac{{2gR}}{{\sqrt 3 }}\]
\[ \Rightarrow {F_C} = \dfrac{{2mg}}{{\sqrt 3 }}\] …… (3)

From the above figure, we can see that only the horizontal component of the centrifugal force will act on the wall OM. Therefore, we have the horizontal component of the centrifugal force is,
\[{F_{cx}} = {F_c}\sin 60^\circ \]
Using equation (3) in the above equation, we get,
\[{F_{cx}} = \dfrac{{2mg}}{{\sqrt 3 }}\sin 60^\circ \]
Substituting 1 kg for m and \[10\,{\text{m/}}{{\text{s}}^2}\]for g in the above equation, we get,
\[{F_{cx}} = \dfrac{{2\left( 1 \right)\left( {10} \right)}}{{\sqrt 3 }} \times \dfrac{{\sqrt 3 }}{2}\]
\[ \therefore {F_{cx}} = 10\,{\text{N}}\]

Therefore, the normal force acting on the wall OM is 10 N.

Note:The weight of the ball and the vertical component of the centrifugal force will not act on the wall OM. In the solution, we have assumed that the position B is close to the wall OM. Note that, it is not the centripetal force that acts in the outward direction on the wall OM but the centrifugal force. The magnitude of these forces is the same but have opposite directions.