Question

A ball of $0.20kg$ hits a wall with a velocity of $25m{{s}^{-1}}$ at an angle of ${{45}^{o}}$. If the ball rebounds at ${{90}^{o}}$ to the direction of incidence, calculate the magnitude of change in momentum of the ball.

Answer 1

Hint: The system of ball and the wall is isolated and the forces acting between them are internal forces. According to the law of conservation of energy, the initial velocity of the ball is equal to the final velocity. Resolving the velocity in their components and then calculating the difference in each direction individually, we can calculate the change in momentum for each direction.
Formulas used:
$p=mv$

Complete answer:
The momentum of a system is calculated as
$p=mv$
Here, $p$ is the momentum of the system
$m$ is the mass
$v$ is the velocity
The figure given below shows the initial situation,

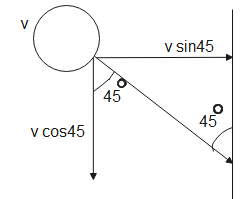
Initially, the ball hits the wall at an angle of ${{45}^{o}}$.
According to the figure, Its momentum in the x-direction will be
$\begin{align}
  & {{p}_{1}}=mv\sin {{45}^{0}} \\
 & \Rightarrow {{p}_{1}}=0.2\times 25\times \dfrac{1}{\sqrt{2}} \\
\end{align}$
$\therefore {{p}_{1}}=2.5\sqrt{2}kg\,m{{s}^{-1}}$ - (1)
Momentum in the y-direction will be-
$\begin{align}
  & p{{'}_{1}}=mv\cos 45 \\
 & \Rightarrow p{{'}_{1}}=0.2\times 25\times \dfrac{1}{\sqrt{2}} \\
\end{align}$
$\therefore p{{'}_{1}}=2.5\sqrt{2}kg\,m{{s}^{-1}}$ - (2)
The figure given below depicts both the initial and final situations,

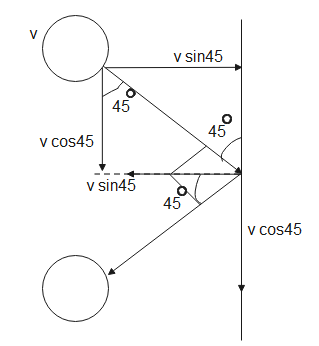
Finally, the ball rebounds at an angle ${{45}^{o}}$ from the normal,
As the system is isolated, the kinetic energy will be conserved, therefore the initial velocity will be equal to the final velocity of the ball.
Its final momentum in the x-direction will be-
$\begin{align}
  & {{p}_{2}}=mv\cos {{45}^{0}} \\
 & \Rightarrow {{p}_{2}}=0.2\times 25\times \dfrac{1}{\sqrt{2}} \\
\end{align}$
$\therefore {{p}_{2}}=2.5\sqrt{2}kg\,m{{s}^{-1}}$ - (3)
The final momentum of the ball in the y-direction will be-
$\begin{align}
  & p{{'}_{2}}=mv\sin 45 \\
 & \Rightarrow p{{'}_{2}}=0.2\times 25\times \dfrac{1}{\sqrt{2}} \\
\end{align}$
$\therefore p{{'}_{2}}=2.5\sqrt{2}kg\,m{{s}^{-1}}$ - (4)

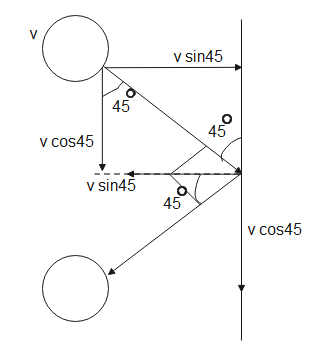
From the figure given above, the initial and final momentum in the y-direction are in the same direction, therefore, from eq (2) and eq (4), the magnitude of change in momentum in the y-direction will be-
$\begin{align}
  & p'=p{{'}_{1}}-p{{'}_{2}} \\
 & \therefore p'=2.5\sqrt{2}-2.5\sqrt{2}=0 \\
\end{align}$
Therefore, the magnitude of change in momentum is 0.
From eq (1) and eq (4), the magnitude of change in momentum in x-direction will be-
$\begin{align}
  & p={{p}_{1}}-{{p}_{2}} \\
 & \Rightarrow p=2.5\sqrt{2}-(-2.5\sqrt{2}) \\
 & \therefore p=5\sqrt{2}kg\,m{{s}^{-1}} \\
\end{align}$
The magnitude of change in momentum is $5\sqrt{2}kg\,m{{s}^{-1}}$ in the x-direction.
Therefore, the magnitude of change in momentum in the x-direction is $5\sqrt{2}kg\,m{{s}^{-1}}$ while in the y-direction, it is 0.

Note:
An isolated system is the system on which no external force acts. For such a system, the law of conservation of energy and momentum applies. Momentum is a vector and its direction is the same as the direction of velocity. The velocity of the ball in the initial and final system is resolved in its corresponding perpendicular components.