Question

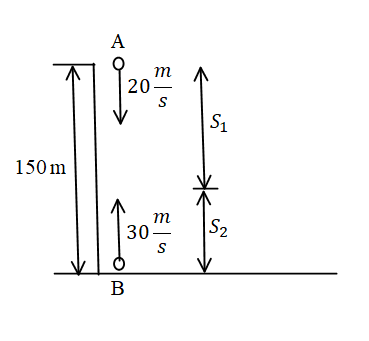
A ball is thrown downwards with a speed of $20\dfrac{m}{s}$ from the top of a building 150 m high and simultaneously another ball is thrown vertically upwards with a speed of $30\dfrac{m}{s}$ from the foot of the building. Find the time after which both the balls will meet. $\left( {g = 10\dfrac{m}{{{s^2}}}} \right)$.

A) $4s$
B) $5s$
C) $3s$
D) $1s$

Answer 1

Hint: The initial velocity of the ball falling from a height 150 m is not zero and also the initial velocity of the ball thrown from the ground is non-zero so it is clear that there will be a collision in between both the ball at some point.

Complete step by step answer:
As it is given that the initial velocity of the ball from height 150 m is $20\dfrac{m}{s}$ and the acceleration acting on the ball is the acceleration due to gravity.
So apply the relation form Newton’s law of motions.
$s = ut + \dfrac{1}{2}a{t^2}$Where s is the displacement, u is the initial velocity, a is the acceleration and t is the time taken.
For the motion of the ball from point A.
${s_A} = {u_A}t + \dfrac{1}{2}a{t^2}$
The acceleration due to gravity would be $a = g$.
$ \Rightarrow {s_1} = {u_1}t + \dfrac{1}{2}g{t^2}$
The value of $g = 10\dfrac{m}{{{s^2}}}$.
$ \Rightarrow {s_1} = 20t + \dfrac{1}{2}10{t^2}$
$ \Rightarrow {s_1} = 20t + 5{t^2}$………eq. (1)
For the motion of the ball from point B.
${s_B} = {u_B}t + \dfrac{1}{2}a{t^2}$
The acceleration due to gravity would be $a = g$.
$ \Rightarrow {s_2} = {u_2}t + \dfrac{1}{2}g{t^2}$
As the acceleration of the body is in the opposite direction, so
$ \Rightarrow {s_2} = {u_2}t - \dfrac{1}{2}g{t^2}$
The initial velocity of the ball from point B is $u = 30\dfrac{m}{s}$ and the value of acceleration due to gravity is equal to $g = 10\dfrac{m}{{{s^2}}}$.
$ \Rightarrow {s_2} = 30t - \dfrac{1}{2}10{t^2}$
$ \Rightarrow {s_2} = 30t - 5{t^2}$………eq. (2)
Since the total distance is equal to 150m,
$ \Rightarrow {s_1} + {s_2} = 150m$
Put the value of ${s_1}$ and ${s_2}$ in the above equation.
$ \Rightarrow \left( {20t + 5{t^2}} \right) + \left( {30t - 5{t^2}} \right) = 150m$
After solving the relation we get,
$ \Rightarrow 20t + 30t = 150m$
$ \Rightarrow 50t = 150m$
On simplification, we get
$ \Rightarrow t = \dfrac{{150}}{{50}}$
$ \Rightarrow t = 3s$

$\therefore$ The time taken by the balls from point A and point B to hit each other will be $t = 3s$. So the correct option is option (C).

Note:
The sign of acceleration due to gravity can be positive and can be negative as well depending upon the direction of the motion of the body. When the ball from the point A is moving towards the ground the sign of acceleration due to gravity is positive because the motion of acceleration due to gravity is as same as the direction of motion of the ball but when the ball from point B towards point A then the direction of motion of the ball is opposite to the direction of the gravity and therefore the sign becomes negative.