Question

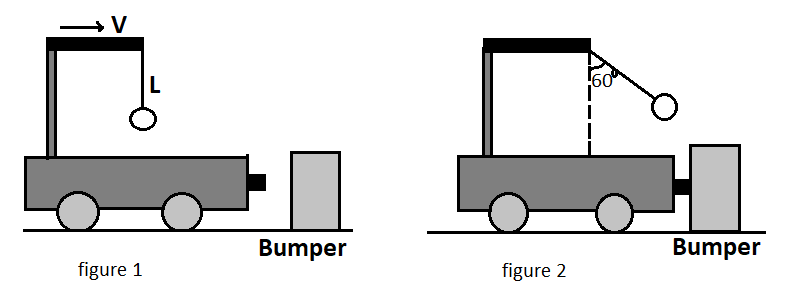
A ball is suspended from the top of a cart by a string of length $1.0\,m$ . The cart and the ball are initially moving to the right at constant speed $V$, as shown in the figure $I$ . The cart comes to rest after colliding and sticking to a fixed bomber, as in figure $II$ . The suspended ball swings through a maximum angle $60^\circ $ . The initial speed $V$ is (take $g = 10\,m{s^{ - 2}}$ )

A. $\sqrt {10} \,m{s^{ - 1}}$
B. $2\sqrt 2 \,m{s^{ - 1}}$
C. $5\sqrt 2 \,m{s^{ - 1}}$
D. $4\,m{s^{ - 1}}$

Answer 1

Hint: The initial velocity is the velocity that the object attains at the starting point. Here, we will use the law of conservation of energy to calculate the initial velocity of the cart. Here, when the cart hits the bumper, the height of the ball from the cart changes because it swings in the forward direction.

Complete step by step answer:
Consider a cart on which a ball is suspended by a string of length $$L = 1.0\,m$$ . Let the cart with the hanging ball is moving with initial velocity $V$ as shown in the figure $I$ . Now, when the cart strikes the bumper, it comes to rest, and the ball swings making an angle of $60^\circ $ . let $h$ be the height to which the ball rises from its original position as shown below

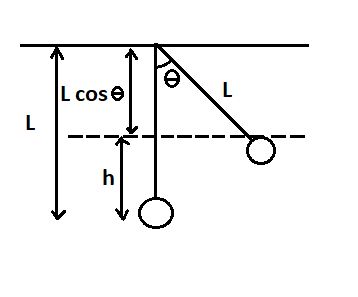
Here, $L\,\cos \theta $ is the length of the string after attaining height $h$ .
Therefore, the height to which the ball rises is given by
$h = L - L\,\cos \theta $
Now, as given in the question, $L = 1$ and $\theta = 60^\circ $
Hence, putting these values in the above equation
$h = 1 - 1 \times \cos 60^\circ $
$ \Rightarrow \,h = 1 - \dfrac{1}{2}$
$ \Rightarrow \,h = \dfrac{1}{2}$
Now, to calculate the initial speed of the cart, we will use the law of conservation of energy as shown below
$K.{E_i} + {U_i} = K.{E_f} + {U_f}$
Now, when the cart comes to rest, the kinetic energy of the ball will be zero.
$\therefore \,K.{E_f} = 0$
Also, at the initial stage, the potential energy of the ball will be zero.
$\therefore \,{U_i} = 0$
Therefore, the law of conservation of energy will become
$K.{E_i} = {U_f}$
$ \Rightarrow \,\dfrac{1}{2} \times m \times v_i^2 = m \times g \times h$
$ \Rightarrow \,\dfrac{1}{2}v_i^2 = g \times h$
$ \Rightarrow \,v_i^2 = 2gh$
$ \Rightarrow \,{v_i} = \sqrt {2gh} $
$ \Rightarrow \,{v_i} = \sqrt {2 \times 10 \times \dfrac{1}{2}} $
$ \Rightarrow \,{v_i} = \sqrt {10} m{s^{ - 1}}$
Therefore, the initial velocity of the cart and the ball is $\sqrt {10} m{s^{ - 1}}$ .

So, the correct answer is “Option A”.

Note:
Now, potential energy is the energy that the object gains at his new position relative to the old position.
Therefore, we have taken potential energy at the initial stage as zero.
Also, kinetic energy is the energy that the object possesses due to its motion.
Therefore, at the initial stage the kinetic energy will be maximum.