Question

A ball is suspended by a thread of length $L$ at the point $O$ on a wall which is inclined to the vertical by $\alpha$. The thread with the ball is displaced by a small angle $\beta$ away from the vertical and also away from the wall. If the ball is released, the period of oscillation of the pendulum when $\beta>\alpha$ will be:
\[\begin{align}
  & A.\sqrt{\dfrac{L}{g}}\left[ \pi +2{{\sin }^{-1}}\dfrac{\alpha }{\beta } \right] \\
 & B.\sqrt{\dfrac{L}{g}}\left[ \pi -2{{\sin }^{-1}}\dfrac{\alpha }{\beta } \right] \\
 & C.\sqrt{\dfrac{L}{g}}\left[ 2{{\sin }^{-1}}\dfrac{\alpha }{\beta }-\pi \right] \\
 & D.\sqrt{\dfrac{L}{g}}\left[ 2{{\sin }^{-1}}\dfrac{\alpha }{\beta }+\pi \right] \\
\end{align}\]

Answer 1

Hint: We know that the time period of an oscillation is dependent on the length of the wire. Here, the wire makes some angle with the vertical wall. Thus we can see that the time period remains unaffected, by the time taken by the oscillation changes.

Formula used:
$T=2\pi\sqrt{\dfrac{L}{g}}$

Complete step-by-step answer:
Let us consider the vertical wall of inclination $\alpha$ to be PQ. And let $\beta$ be the angle made by the pendulum with the mean position OA. Let the position of ball at any time $t$ be given as, $x(t)=A cos\omega t$. Then, the angular displacement $\theta$ is given as $\theta=\beta cos(\omega t)$
We know that the time period of an oscillation is given as $T=2\pi\sqrt{\dfrac{L}{g}}$
Clearly, if $\beta > \alpha$, then the ball will collide with the wall. If the ball rebounds, with the same speed, then the time period of the oscillation is two times the normal oscillation of a simple pendulum system.

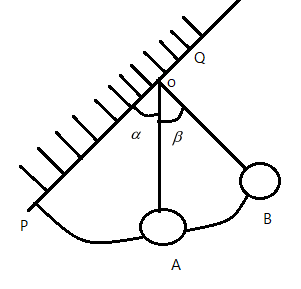
Let us consider $t_{1}$ to the time taken for the pendulum during the collision, then $t_{1}=\dfrac{T}{2}=\dfrac{2\pi\sqrt{\dfrac{L}{g}}}{2}=\pi\sqrt{\dfrac{L}{g}}$.
Then the time taken during the angular displacement $\alpha$ is given as $\alpha=\beta sin(\omega t_{2})$. Clearly, this is the time taken to return to the mean position.
$\implies t_{2}=\dfrac{1}{\omega}sin^{-1}\left(\dfrac{\alpha}{\beta}\right)$. We know that $\dfrac{1}{\omega}=\sqrt{\dfrac{L}{g}}$
Then, the time taken to return to the mean position$t_{2}$ becomes, $t_{2}=\sqrt{\dfrac{L}{g}}sin^{-1}\left(\dfrac{\alpha}{\beta}\right)$. Then the time taken for the complete oscillation is, $2t_{2}$
Clearly, the total oscillation of the ball is $t=t_{1}+t_{2}=\pi\sqrt{\dfrac{L}{g}}+2\sqrt{\dfrac{L}{g}}sin^{-1}\left(\dfrac{\alpha}{\beta}\right)$.
$\implies t=\sqrt{\dfrac{L}{g}}\left[\pi+2sin^{-1}\left(\dfrac{\alpha}{\beta}\right)\right]$
Thus the correct answer is \[A.\sqrt{\dfrac{L}{g}}\left[ \pi +2{{\sin }^{-1}}\dfrac{\alpha }{\beta } \right]\]

So, the correct answer is “Option A”.

Note: Option D and A looks similar. But A is the correct answer, as $\beta > \alpha$, we can say that the ball undergoes oscillation first. Thus, the time taken due to the oscillation of $\beta$ is taken first, when compared to that of the $\alpha$.