Question

A ball falls on an inclined plane of inclination from height h above the point of impact and makes a perfectly elastic collision, where will it hit the plane again?

Answer 1

Hint: We will form a correct diagram which can be done according to the information given and we will use the formulas of kinematics of displacement in vertical and horizontal directions. After that, we will find the length of the ball coming back again to the inclined plane.

Formula used:
${{v}_{\text{o}}}=\sqrt{2gh}$ where g is gravitational force, h is height, $Vertical\,height={{v}_{\text{o }\left( \text{vertical} \right)}}t+\dfrac{1}{2}\left( \text{ver}\text{.}\, \right)\text{acceleration}\left( {{t}^{2}} \right)$ , vertical height is 0, ${{v}_{\text{o }\left( vertical \right)}}={{v}_{\text{o}}}\cos \left( \theta \right)$ and ${{a}_{y}}=-g\cos \left( \theta \right)$ ,$x={{v}_{\text{o }\left( \text{horizontal} \right)}}t+\dfrac{1}{2}{{a}_{x}}{{t}^{2}}$ , x is l units, ${{v}_{\text{o }\left( \text{horizontal} \right)}}={{v}_{\text{o}}}\sin \left( \theta \right)$ and ${{a}_{x}}=g\sin \left( \theta \right)$

Complete answer:
We will consider the following diagram.
 

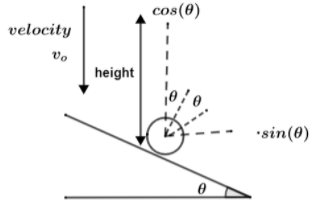
The plane on which the ball hits is slightly inclined. We will suppose that the ball strikes the plane with velocity of ${{v}_{\text{o}}}$. As this velocity includes height and force of gravity so, ${{v}_{\text{o}}}=\sqrt{2gh}$. Therefore, we have equation in two dimension as $Vertical\,height={{v}_{\text{o }\left( \text{vertical} \right)}}t+\dfrac{1}{2}\left( \text{ver}\text{.}\, \right)\text{acceleration}\left( {{t}^{2}} \right)$. By taking vertical height as y and ver. Acceleration as ${{a}_{y}}$ so we get
$y={{v}_{\text{o }\left( \text{vertical} \right)}}t+\dfrac{1}{2}{{a}_{y}}{{t}^{2}}$
As vertical height is 0, ${{v}_{\text{o }\left( vertical \right)}}={{v}_{\text{o}}}\cos \left( \theta \right)$ and ${{a}_{y}}=-g\cos \left( \theta \right)$ therefore, $0={{v}_{\text{o}}}\cos \left( \theta \right)t-\dfrac{1}{2}g\cos \left( \theta \right){{t}^{2}}$
$\Rightarrow -\dfrac{1}{2}g\cos \left( \theta \right){{t}^{2}}+{{v}_{\text{o}}}\cos \left( \theta \right)t=0$
$\Rightarrow -g\cos \left( \theta \right){{t}^{2}}+2{{v}_{\text{o}}}\cos \left( \theta \right)t=0$
Therefore, we get
$\Rightarrow t\left( -g\cos \left( \theta \right)t+2{{v}_{\text{o}}}\cos \left( \theta \right) \right)=0$
$\Rightarrow t=0\,\,or\,\,-g\cos \left( \theta \right)t+2{{v}_{\text{o}}}\cos \left( \theta \right)=0$
$\Rightarrow t=0\,\,or\,\,-g\cos \left( \theta \right)t=-2{{v}_{\text{o}}}\cos \left( \theta \right)$
$\Rightarrow t=0\,\,or\,\,t=2\dfrac{{{v}_{\text{o}}}\cos \left( \theta \right)}{g\cos \left( \theta \right)}$
$\Rightarrow t=0\,\,or\,\,t=2\dfrac{{{v}_{\text{o}}}}{g}$
Now, similarly horizontal displacement is $x={{v}_{\text{o }\left( \text{horizontal} \right)}}t+\dfrac{1}{2}{{a}_{x}}{{t}^{2}}$. Let the horizontal distance covered by the ball is l units so, x is l units, ${{v}_{\text{o }\left( \text{horizontal} \right)}}={{v}_{\text{o}}}\sin \left( \theta \right)$ and ${{a}_{x}}=g\sin \left( \theta \right)$ therefore,$l={{v}_{\text{o}}}\sin \left( \theta \right)t+\dfrac{1}{2}g\sin \left( \theta \right){{t}^{2}}$. As $t=2\dfrac{{{v}_{\text{o}}}}{g}$ so,
$l={{v}_{\text{o}}}\sin \left( \theta \right)\left( 2\dfrac{{{v}_{\text{o}}}}{g} \right)+\dfrac{1}{2}g\sin \left( \theta \right){{\left( 2\dfrac{{{v}_{\text{o}}}}{g} \right)}^{2}}$
$\Rightarrow l={{v}_{\text{o}}}\sin \left( \theta \right)\left( 2\dfrac{{{v}_{\text{o}}}}{g} \right)+\dfrac{1}{2}g\sin \left( \theta \right){{\left( 2\dfrac{{{v}_{\text{o}}}}{g} \right)}^{2}}$
 $\Rightarrow l={{v}_{\text{o}}}\sin \left( \theta \right)\left( 2\dfrac{{{v}_{\text{o}}}}{g} \right)+\sin \left( \theta \right)\times {{v}_{\text{o}}}\times 2\dfrac{{{v}_{\text{o}}}}{g}$
$\Rightarrow l=\dfrac{2{{v}_{\text{o}}}^{2}\sin \left( \theta \right)}{g}+\dfrac{2{{v}_{\text{o}}}^{2}\sin \left( \theta \right)}{g}$
$\Rightarrow l=\dfrac{4{{v}_{\text{o}}}^{2}\sin \left( \theta \right)}{g}$
 Since, ${{v}_{\text{o}}}=\sqrt{2gh}$ so,
$l=\dfrac{4{{\left( \sqrt{2gh} \right)}^{2}}\sin \left( \theta \right)}{g}$
$\Rightarrow l=\dfrac{4\left( 2gh \right)\sin \left( \theta \right)}{g}$
$\Rightarrow l=8h\sin \left( \theta \right)$
Hence, the ball will again hit the inclined plane by getting a bounce off l length at $l=8h\sin \left( \theta \right)$ position.

Note:
Diagrams play an important part for this question. If the figure is incorrect then this means that the diagram is also incorrectly interpreted. Because the height here is taken as displacement so, this is actually due to the flat of the ball coming back to its position vertically. The value of time t = 0 is not considered here forward because of some action done in time t. So, definitely it will have some value of time. That is why the time is taken as $t=2\dfrac{{{v}_{\text{o}}}}{g}$. Vertical displacement is zero but horizontal is not because the horizontal position of the ball is not coming back to its original position due to the inclined plane.