Question

A bag of mass \[M\] hangs by a long massless rope. A bullet of mass \[m\] , moving horizontally with velocity \[u\] , is caught in the bag. Then for the combined (bag+bullet) system, just after the collision:
(A) Momentum is \[muM/(M+m)\]
(B) Kinetic energy is \[m{{u}^{2}}/2\]
(C) Momentum is \[mu(M+m)/M\]
(D) Kinetic energy is \[{{m}^{2}}{{u}^{2}}/2(M+m)\]

Answer 1

Hint:-This is a classic example of a question where we have to apply momentum conservation theorem. In the given question, inelastic collision is taking place, hence we cannot apply the energy conservation theorem. Energy conservation can be applied only in case of an elastic collision.

Complete Step by Step Solution:
According to momentum conservation, momentum before the collision = momentum after the collision.
Substituting the respective values, we get the equation, \[mu=(M+m)v\] where \[v\] is the final velocity of the (bullet+bag) system. Therefore, momentum after collision \[=(M+m)v=mu\]and velocity after the collision \[v=mu/(M+m)\]
The above analysis might be little cumbersome to understand, so look at the following diagram and visualise the collision for better understanding

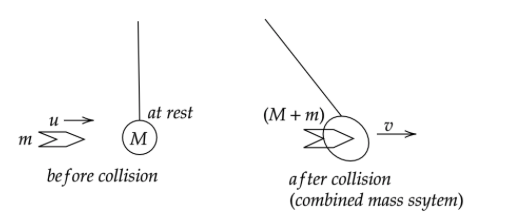
Now go through the momentum conservation analysis given above once again and it’ll all seem a cakewalk to you.
Now that you’ve understood momentum conservation, we should move further and calculate kinetic energy
Hence Kinetic energy after the collision \[=1/2(M+m){{v}^{2}}\]
Substituting the value of v, we get kinetic energy as \[\dfrac{1}{2}(M+m)\dfrac{{{m}^{2}}{{u}^{2}}}{{{(M+m)}^{2}}}=\dfrac{{{m}^{2}}{{u}^{2}}}{2(M+m)}\]

Therefore, option (D) is the correct answer

Note:We can also approach this question with the help of newton’s equation for a collision which states that relative velocity of recession (after collision) = \[e\] * relative velocity of approach (before the collision), where \[e\] is the coefficient of the collision, if the value of \[e\] is one, the collision is elastic and if the value of \[e\] is zero, the collision is said to be inelastic.
Although I would recommend simple momentum conservation because it’s shorter and simpler and will save you some precious time.