Question

A bacterial infection in an internal wound grows as $N\prime (t)={{N}_{O}}{{\exp }^{(t)}}$, where the time ‘t’ is in hours. A dose of antibiotic, taken orally, needs one hour to reach the wound. Once it reaches there, the bacterial population goes down as $\dfrac{dN}{dt}=-5{{N}^{2}}$. What will be the plot of $\dfrac{{{N}_{0}}}{N}$ vs t after one hour?
A.

B.
                 

C.
             

D.
                 

Answer 1

Hint:. To solve this question, first find out the bacterial growth at time equals to one hour. The bacterial growth from one hour onwards is already given. Then find out the bacterial at time equals to t hours. You have to use integration and then find the type of equation.

Complete step by step answer:
Given that,
A bacterial infection in an internal wound grows as ${{N}^{'}}(t)={{N}_{O}}{{\exp }^{(t)}}$, where the time ‘t’ is in hours. A dose of antibiotic, which is taken orally, needs one hour to reach the wound and once it reaches there, the bacterial population becomes $\dfrac{dN}{dt}=-5{{N}^{2}}$. We have to find out the plot of $\dfrac{{{N}_{0}}}{N}$ vs t after one hour.

So, from $0$ to $1$ hour, the bacterial growth is $N\prime ={{N}_{0}}{{e}^{t}}$.
So, at $t=1$ hour, the bacterial growth will be $N\prime =e{{N}_{0}}$.
And from one hour onwards, the bacterial growth becomes $\dfrac{dN}{dt}=-5{{N}^{2}}$.
In the given equation $\dfrac{dN}{dt}=-5{{N}^{2}}$, let’s take ${{N}^{2}}$ to the denominator in the left side and $dt$ to the right side. Then we will get:
$\dfrac{dN}{{{N}^{2}}}=-5dt$

Let the bacterial growth at t time be ‘N’.
So, by integrating the above reaction from ${{N}_{0}}e$ to $N$, we will get:
$\int\limits_{{{N}_{0}}e}^{N}{\dfrac{dN}{{{N}^{2}}}=\int\limits_{1}^{t}{-5dt}}$
Then, $\int\limits_{{{N}_{0}}e}^{N}{{{N}^{-2}}dN=-5\int\limits_{1}^{t}{dt}}$

Then, after multiplying ${{N}_{0}}$ on both side we get:
$\dfrac{{{N}_{0}}}{N}-\dfrac{1}{e}=5{{N}_{0}}(t-1)$
Then, $\dfrac{{{N}_{0}}}{N}=5{{N}_{0}}(t-1)+\dfrac{1}{e}$

And, the final equation will be:
$\dfrac{{{N}_{0}}}{N}=5{{N}_{0}}t+\left( \dfrac{1}{e}-5{{N}_{0}} \right)$
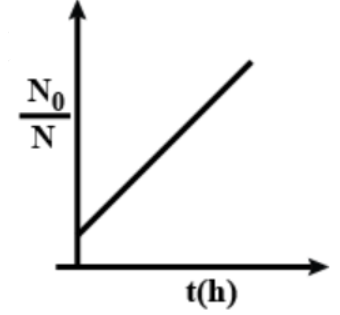
Here, if we consider $\dfrac{{{N}_{0}}}{N}$ as y-axis, $5{{N}_{0}}$ as m, $t$ as the x-axis and $\left( \dfrac{1}{e}-5{{N}_{0}} \right)$ as c, the plot equation will be $y=mx+c$ which represent an increasing straight line. And option A shows an increasing straight line (i.e. positive slope) in the plot.
So, the correct answer is “Option A”.

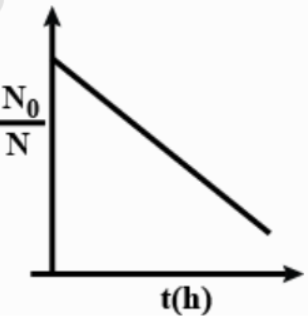
Note: The possible mistake is that you can get confused with option B which shows a negative slope but is a straight line. The plot equation for such a plot can be represented by $y=mx-c$ and it is generally shown by a decreasing straight line in the plot.