Question

A baby crawls $ 8 $ feet towards the west and then $ 8 $ feet towards the north. If then moves $ 14 $ feet towards the east. How far and in which direction is the baby from the starting point?

Answer 1

Hint: As we know that the above given question is a word problem. A problem is a mathematical question written as one sentence or more describing a real life scenario where that problem needs to be solved by the way of mathematical calculation. We can solve the given problem by applying the method of equation and then solve it.

Complete step-by-step answer:
We need to first understand the requirement of the question which is the distance between the starting and ending point.
When a baby crawls $ 8 $ feet towards turns north, Finally he turns $ 14 $ feet towards east. It makes a right angled triangle.
The sides will be $ 8cm $ and $ 14 - 8 = 6cm $ .
Let us first draw the diagram of the direction and then we can draw the figure according to the question.

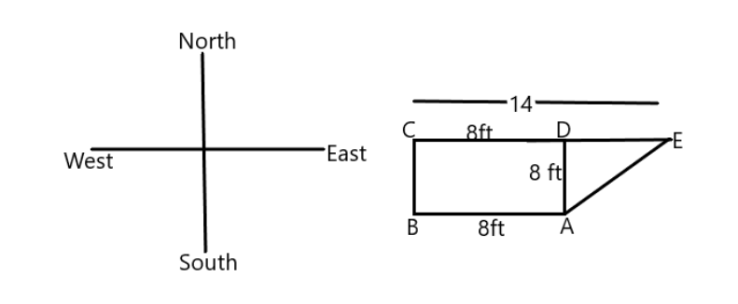
In the above figure we can see that we have $ CE = 14 $ and $ CD = 8 $ , so we have $ DE = 14 - 8 = 6 $ .
Also all the sides of a square are equal, here ABCD is a square so $ AB = CD = BC = AD = 8ft $ .
We have now ADE is a right angled triangle. Here we have to find the distance from point A to point E, which is the hypotenuse of the triangle.
From the Pythagoras theorem, we can write it as $ $ $ {8^2} + {6^2} = {x^2} $ .
Now we solve this; $ 64 + 36 = {x^2} \Rightarrow x = \sqrt {100} = 10 $
Hence the distance between the starting point and ending point is $ 10 $ m.
So, the correct answer is “10 m”.

Note: We should always be careful what the question is asking i.e. is it asking the distance between the two points. Based on the requirement and by observing all the necessary information that is already available in the question we gather the information and then create an equation or by unitary method whichever is applicable, then we solve the problem and then verify the answer by putting the value in the problem and see whether we get the same answer or not.