Question

A, B, C, D,…. are n points in a plane whose coordinates are \[\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right),\left( {{x}_{3}},{{y}_{3}} \right),.......\] AB is bisected in the point \[{{G}_{1}};{{G}_{1}}C\] is divided at \[{{G}_{2}}\] in the ratio 1 : 2, \[{{G}_{2}}D\] is divided at \[{{G}_{3}}\] in the ratio 1 : 3, \[{{G}_{3}}E\] at \[{{G}_{4}}\] in the ratio 1 : 4, and so on until all the points are exhausted. Show that the coordinates of the final point so obtained are: - \[\dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}+....+{{x}_{n}}}{n}\] and \[\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}+....+{{y}_{n}}}{n}\]. [This point is called the centre of Mean Position of the n given points].

Answer 1

Hint: First consider points A and B and use the mid – point formula given as: - \[\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)\], to calculate the coordinates of \[{{G}_{1}}\]. Here, \[\left( {{x}_{1}},{{y}_{1}} \right)\] are the coordinates of A and \[\left( {{x}_{2}},{{y}_{2}} \right)\] are the coordinates of B. Now, consider a line joining the points \[{{G}_{1}}\] and C which is divided at \[{{G}_{2}}\] in the ratio 1 : 2. Use section formula given as: - \[\left( \dfrac{M{{X}_{2}}+N{{X}_{1}}}{M+N},\dfrac{M{{Y}_{2}}+N{{Y}_{1}}}{M+N} \right)\] to calculate the coordinates of \[{{G}_{2}}\]. Here, M : N is the ratio in which line is divided and \[\left( {{X}_{1}},{{Y}_{1}} \right),\left( {{X}_{2}},{{Y}_{2}} \right)\] are the coordinates of \[{{G}_{1}},C\] respectively. Use the same section formula to calculate the coordinates of \[{{G}_{3}},{{G}_{4}}\] and observe the general pattern to get the coordinates of \[{{G}_{n}}\].

Complete step-by-step solution
Here, we have been provided with ‘n’ points: - A, B, C, D ….. n having coordinates \[\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right),\left( {{x}_{3}},{{y}_{3}} \right),.....\], where \[\left( {{x}_{1}},{{y}_{1}} \right)\] and \[\left( {{x}_{2}},{{y}_{2}} \right)\] are the coordinates of A and B respectively, we get,
 

\[\Rightarrow \] x – coordinate of \[{{G}_{1}}=\dfrac{{{x}_{1}}+{{x}_{2}}}{2}\]
\[\Rightarrow \] y – coordinate of \[{{G}_{1}}=\dfrac{{{y}_{1}}+{{y}_{2}}}{2}\]
Now, it is given that \[{{G}_{1}}C\] is divided at \[{{G}_{2}}\] in the ratio 1 : 2.
So, we have,

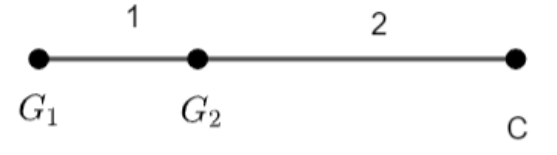
Using the section formula given as: - \[\left( \dfrac{M{{X}_{2}}+N{{X}_{1}}}{M+N},\dfrac{M{{Y}_{2}}+N{{Y}_{1}}}{M+N} \right)\] to calculate the coordinates of \[{{G}_{2}}\], where M : N is the ratio in which \[{{G}_{1}}C\] is divided and \[\left( {{X}_{1}},{{Y}_{1}} \right)\] and \[\left( {{X}_{2}},{{Y}_{2}} \right)\] are the coordinates of \[{{G}_{1}}\] and C respectively, we get,
\[\Rightarrow M:N=1:2\]
\[\Rightarrow \] Coordinates of C = \[\left( {{x}_{3}},{{y}_{3}} \right)=\left( {{X}_{2}},{{Y}_{2}} \right)\]
\[\Rightarrow \] Coordinates of \[{{G}_{1}}=\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)=\left( {{X}_{1}},{{Y}_{1}} \right)\]
\[\Rightarrow \] x – coordinate of \[{{G}_{2}}\] = \[\dfrac{2\times \left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2} \right)+1\times {{x}_{3}}}{2+1}\]
\[\Rightarrow \] x – coordinate of \[{{G}_{2}}\] = \[\dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3}\]
\[\Rightarrow \] y – coordinate of \[{{G}_{2}}\] = \[\dfrac{2\times \left( \dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)+1\times {{y}_{3}}}{2+1}\]
\[\Rightarrow \] y – coordinate of \[{{G}_{2}}\] = \[\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3}\]
Now, we have been given that \[{{G}_{2}}D\] is divided at \[{{G}_{3}}\] in ratio 1: 3. So, we have,

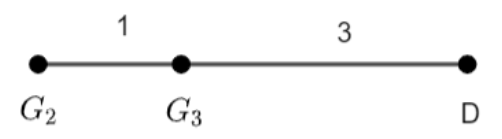
Using the section formula, we get,
\[\Rightarrow M:N=1:3\]
\[\Rightarrow \] Coordinates of D = \[\left( {{x}_{4}},{{y}_{4}} \right)=\left( {{X}_{2}},{{Y}_{2}} \right)\]
\[\Rightarrow \] Coordinates of \[{{G}_{2}}=\left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right)=\left( {{X}_{1}},{{Y}_{1}} \right)\]
\[\Rightarrow \] x – coordinate of \[{{G}_{3}}=\dfrac{3\times \left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3} \right)+1\times {{x}_{4}}}{3+1}\]
\[\Rightarrow \] x – coordinate of \[{{G}_{3}}=\dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}+{{x}_{4}}}{4}\]
Similarly, y – coordinate of \[{{G}_{3}}=\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}+{{y}_{4}}}{4}\]
Therefore, on observing the pattern we can write the coordinates of \[{{G}_{4}},{{G}_{5}},....\] easily.
On observing the series in the question we can say that the line joining the points \[{{G}_{\left( n-2 \right)}}\] and n will be divided by \[{{G}_{n}}\] in the ratio of 1 : (n - 1). Therefore, we have,

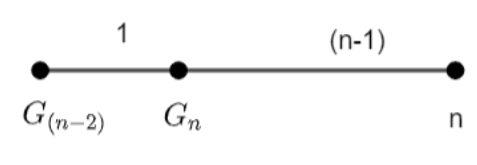
Here, M : N = 1 : (n - 1)
\[\Rightarrow \] Coordinates of \[n=\left( {{x}_{n}},{{y}_{n}} \right)=\left( {{X}_{2}},{{Y}_{2}} \right)\]
\[\Rightarrow \] Coordinates of \[{{G}_{\left( n-2 \right)}}=\left( \dfrac{{{x}_{1}}+{{x}_{2}}+.....+{{x}_{n-1}}}{n-1},\dfrac{{{y}_{1}}+{{y}_{2}}+....+{{y}_{n-1}}}{n-1} \right)=\left( {{X}_{1}},{{Y}_{1}} \right)\]
So, applying the section formula, we get,
\[\Rightarrow \] x – coordinate of \[{{G}_{n}}=\dfrac{\left( n-1 \right)\times \left( \dfrac{{{x}_{1}}+{{x}_{2}}+.....+{{x}_{n-1}}}{n-1} \right)+1\times {{x}_{n}}}{1+\left( n-1 \right)}\]
\[\Rightarrow \] x – coordinate of \[{{G}_{n}}=\dfrac{{{x}_{1}}+{{x}_{2}}+.....+{{x}_{n-1}}+{{x}_{n}}}{1+\left( n-1 \right)}\]
Similarly, y – coordinate of \[{{G}_{n}}=\dfrac{{{y}_{1}}+{{y}_{2}}+......+{{y}_{n-1}}+{{y}_{n}}}{n}\]
Here, \[{{G}_{n}}\] will be the final point whose coordinates are: - \[\dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}.....+{{x}_{n}}}{n}\] and \[\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}.....+{{y}_{n}}}{n}\].
Hence, proved

Note: One must note that it is not possible for us to determine the coordinates of each of the points \[{{G}_{1}},{{G}_{2}},{{G}_{3}},....\] up to \[{{G}_{n}}\] using the formula again and again. That is why we have to identify the general expression for the points. You must remember the question. Remember that the midpoint formula is a special case of section formula where M: N = 1: 1.