Question

a, b are the intercepts made by a line on the axes such that $\dfrac{1}{a} + \dfrac{1}{b} = \dfrac{1}{c}$. Then the line passes through the points
A.(1,1)
B.(a,a)
C.(c,c)
D.$\left( {\dfrac{1}{c},\dfrac{1}{c}} \right)$

Answer 1

Hint: In this question, we need to determine the coordinates of the point through which the line passes, making an intercept of a and b on the axes. For this, we will establish the equation of the line first and then compare the same with the given condition in the question $\dfrac{1}{a} + \dfrac{1}{b} = \dfrac{1}{c}$.

Complete step-by-step answer:
Let the line make an intercept of ‘a’ on the x-axis and ‘b’ on the y-axis such. The following figure depicts the same.

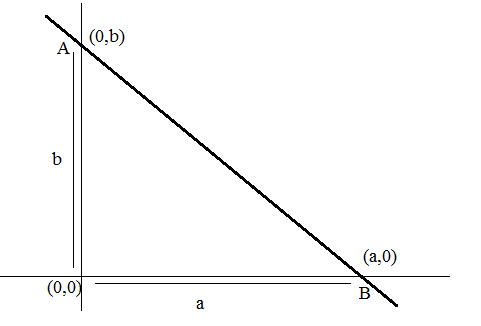
From the figure, we can see that the coordinates of points A and B are given as A(0,b) and B(a,0), respectively.
Following the property of the equation of the line segment joining two points is given as:
$\Rightarrow y - {y_1} = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\left( {x - {x_1}} \right)$ where $\left( {{x_1},{y_1}} \right)$ and $\left( {{x_2},{y_2}} \right)$ are the endpoints of the line segments.
Here, $ \left( {{x_1},{y_1}} \right) \equiv \left( {0,b} \right)$ and $\left( {{x_2},{y_2}} \right) \equiv \left( {a,0} \right)$. So, substitute these values in the equation $\Rightarrow y - {y_1} = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\left( {x - {x_1}} \right)$ to establish the equation of the line segment AB.
$
\Rightarrow y - {y_1} = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\left( {x - {x_1}} \right) \\
\Rightarrow y - b = \dfrac{{0 - b}}{{a - 0}}\left( {x - 0} \right) \\
\Rightarrow y - b = \dfrac{{ - bx}}{a} \\
 $
Rearranging the terms in the above equation, we get
$
\Rightarrow y - b = \dfrac{{ - bx}}{a} \\
\Rightarrow ya - ab = - bx \\
\Rightarrow bx + ay = ab - - - - (i) \\
 $
It is given in the question that the line also follows the equation $\dfrac{1}{a} + \dfrac{1}{b} = \Rightarrow \dfrac{1}{c}$ , so, rearranging the given equation, we get
$
\Rightarrow \dfrac{1}{a} + \dfrac{1}{b} = \dfrac{1}{c} \\
\Rightarrow \dfrac{{a + b}}{{ab}} = \dfrac{1}{c} \\
\Rightarrow ac + bc = ab - - - - (ii) \\
 $
Now, comparing the equations (i) and (ii), we get
$
\Rightarrow bx + ay = ab{\text{ and }}ab = ac + bc \\
\Rightarrow bx + ay = ac + bc \\
\Rightarrow x = c{\text{ and }}y = c \\
 $
Hence, $(x,y) \equiv (c,c)$
As, x and y are the coordinates on the line segment AB so, the line will pass through (x,y), which is equivalent to (c,c).
Hence, we can say that the line will pass through the point (c,c).

So, the correct answer is “Option C”.

Note: Here, we have taken a and b as the intercept on the x and y- axes, respectively, but the students can also take a as the y-intercept and b as the x-intercept. It will not change the answer. Moreover, the selection of the points $({x_1},{y_1})$ can also be taken as either of the endpoints of the line AB.