Question

A, B and C are three collinear points. The coordinates of A and B are $ \left( 3,4 \right) $ and $ \left( 7,7 \right) $ respectively and $ AC=10 $ units. Find the sum of the coordinates of C.

Answer 1

Hint: If three points A, B and C are collinear in that order, then $ AB+BC=AC $.
The section formula gives the coordinates of a point $ P\left( x,y \right) $ which divides the line joining two points $ A\left( {{x}_{1}},{{y}_{1}} \right) $ and $ B\left( {{x}_{2}},{{y}_{2}} \right) $ in the ratio $ AP:PB=m:n $, internally or externally.
For internal division: $ P(x,y)=\left( \dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right) $.
For external division: $ P(x,y)=\left( \dfrac{m{{x}_{2}}-n{{x}_{1}}}{m-n},\dfrac{m{{y}_{2}}-n{{y}_{1}}}{m-n} \right) $.
The distance between two points $ A\left( {{x}_{1}},{{y}_{1}} \right) $ and $ B\left( {{x}_{2}},{{y}_{2}} \right) $ can be calculated by using the Pythagoras' theorem. It is given by $ A{{B}^{2}}={{({{x}_{1}}-{{x}_{2}})}^{2}}+{{({{y}_{1}}-{{y}_{2}})}^{2}} $.
Assume the coordinates of C to be $ \left( x,y \right) $. Use the section formula to find the values of $ x $ and $ y $.

Complete step by step answer:
The two given points are $ A\left( 3,4 \right) $ and $ B\left( 7,7 \right) $. Let's say that the coordinates of the third point are $ C\left( x,y \right) $.
We can find the distance AB using the formula for the distance:
 $ A{{B}^{2}}={{(3-7)}^{2}}+{{(4-7)}^{2}} $
⇒ $ A{{B}^{2}}={{4}^{2}}+{{3}^{2}} $
⇒ $ A{{B}^{2}}=16+9 $
⇒ $ A{{B}^{2}}=25 $
⇒ $ AB=5 $
We are also given that $ AC=10 $.
Since the points are given to be collinear and $ AC>AB $, either A is between B and C or B is between A and C. The two positions of the point C are shown in the diagram below:

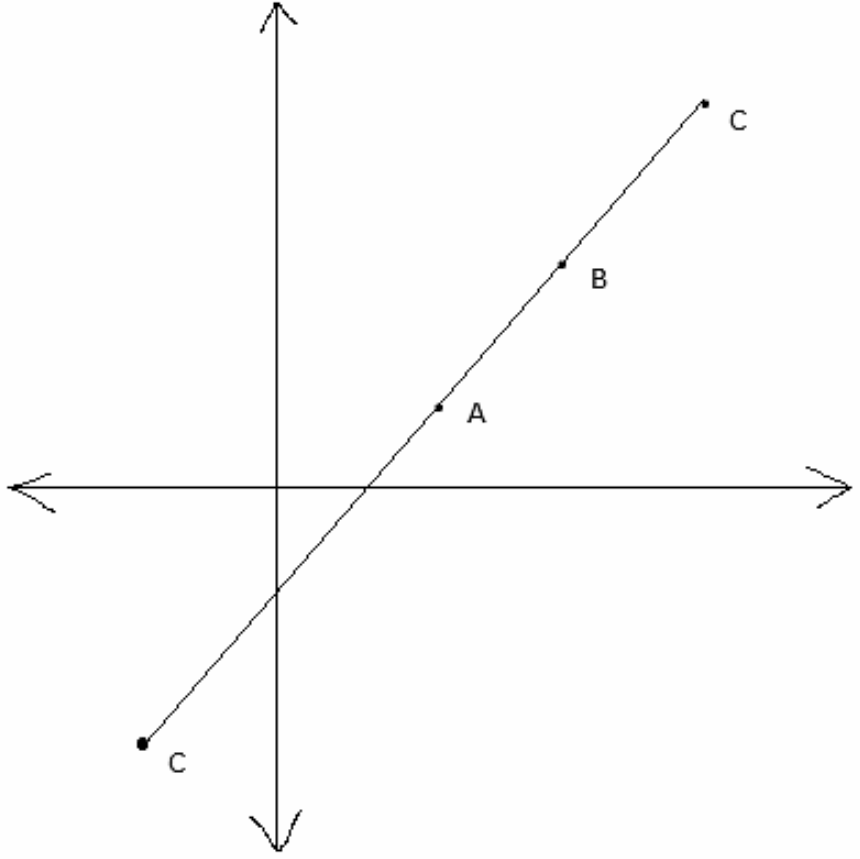
We have the following two cases:
CASE 1: A divides BC in the ratio $ BA:AC=5:10=1:2 $ internally.
Using the section formula, $ A(3,4)=\left( \dfrac{2(7)+1(x)}{2+1},\dfrac{2(7)+1(y)}{2+1} \right) $.
⇒ $ 3=\dfrac{14+x}{3} $ and $ 4=\dfrac{14+y}{3} $
⇒ $ 9=14+x $ and $ 12=14+y $
⇒ $ x=-5 $ and $ y=-2 $
CASE 2: B divides AC in the ratio $ AB:BC=5:5=1:1 $ internally.
Using the section formula, $ B(7,7)=\left( \dfrac{1(3)+1(x)}{1+1},\dfrac{1(4)+1(y)}{1+1} \right) $.
⇒ $ 7=\dfrac{3+x}{2} $ and $ 7=\dfrac{4+y}{2} $
⇒ $ 14=3+x $ and $ 14=4+y $
⇒ $ x=11 $ and $ y=10 $
Therefore, the coordinates of C are either $ C\left( -5,-2 \right) $ or $ C\left( 11,10 \right) $.
The sum of the coordinates of C will be either $ -5+(-2)=-7 $ or $ 11+10=21 $.

Note: The question can also be solved using the distance formula.
For three points $ A\left( {{x}_{1}},{{y}_{1}} \right) $, $ B\left( {{x}_{2}},{{y}_{2}} \right) $ and $ C\left( {{x}_{3}},{{y}_{3}} \right) $ to be collinear, the slope of each line segment should be same. i.e. $ \dfrac{{{x}_{1}}-{{x}_{2}}}{{{y}_{1}}-{{y}_{2}}}=\dfrac{{{x}_{2}}-{{x}_{3}}}{{{y}_{2}}-{{y}_{3}}}=\dfrac{{{x}_{3}}-{{x}_{1}}}{{{y}_{3}}-{{y}_{1}}} $.
There are many ways to show that three points A, B and C are collinear (in a straight line):
Section formula (Ratio / Slope method).
Distance method: $ AB+BC=AC $.
Area method: $ \text{Area of }\Delta ABC=0 $.