Question

(a) At what height above Earth’s Surface is the energy required to lift a satellite to that height equal to the kinetic energy required for the satellite to be in orbit at that height.
(b) For greater heights, which is greater, the energy for lifting or the kinetic energy for orbiting.

Answer 1

Hint: In this question, we have to find the energy required to move a particle at a distance from the surface of the Earth. Then we have to find the kinetic energy required to raise a satellite to move in an orbit. Then according to the question, both the energies are equal. We have to just compare the equations and hence find the answer.

Complete step by step answer:

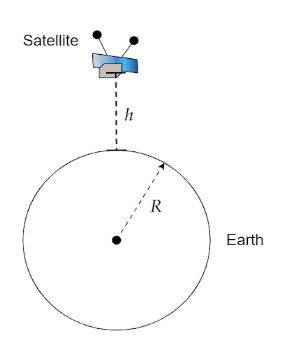
Let the height at which the satellite is kept be $h$ from the surface of Earth. The energy which is required to lift the satellite is potential energy. Thus the difference in potential energy from its final position to its initial position gives the energy which is required to take it to that height.

Initial potential energy $U$ at the surface of Earth.
$U = - \dfrac{{GMm}}{R}$
where $G = $ Universal Gravitational Constant, $M = $ Mass of the Earth, $m = $ mass of the satellite and $R = $ Radius of the Earth.
Potential energy at height $h$ from the surface of Earth is,
$U' = - \dfrac{{GMm}}{{R + h}}$
So, the energy required to lift the satellite to height $h$ is,
$U' - U = - \dfrac{{GMm}}{{R + h}} + \dfrac{{GMm}}{R} \\
\Rightarrow U' - U= GMm\left[ {\dfrac{h}{{R\left( {R + h} \right)}}} \right] - - - - - \left( 1 \right)$

Now, let us find the kinetic energy required to keep the satellite at that state.
The centripetal force that acts on the satellite is equal to the force of gravitation, that’s why it revolves around it.Therefore,
$\dfrac{{m{v^2}}}{{R + h}} = \dfrac{{GMm}}{{{{\left( {R + h} \right)}^2}}}$
Multiplying $\dfrac{1}{2}\left( {R + h} \right)$ in both sides we get,
$\dfrac{1}{2}m{v^2} = \dfrac{{GMm}}{{2\left( {R + h} \right)}}$
So, the kinetic energy required to keep the satellite in that position is $\dfrac{{GMm}}{{2\left( {R + h} \right)}}$.

According to the question, the kinetic energy and potential energy are equal.
$\dfrac{{GMm}}{{2\left( {R + h} \right)}} = GMm\left[ {\dfrac{h}{{R\left( {R + h} \right)}}} \right]$
Solving the equation we get,
$h = \dfrac{R}{2}$
The radius of earth is $6400{\text{ }}km$.
$ h = \dfrac{{6400}}{2} \\
\Rightarrow h= 3200 \\
\therefore h= 3.2 \times {10^6}{\text{ }}m$

(b) For greater heights, $h' > h$, the potential energy required will be more. Thus, the energy of lifting will be more.

Note: It must be noted that the initial kinetic energy required to position the satellite at that height is not as equal to the energy asked in the question. Or else we would imply the conservation of total energy of a system remains conserved. The potential energy is in negative sign as it implies the direction.