Question

A and B start a two-length swimming race at the same moment but from opposite ends of the pool. They swim in lanes at uniform speeds, but A is faster than B. They first pass at a point 18.5 m from the deep end and having completed one length each 1 is allowed to rest on the edge for exactly 45 sec. After setting off on the return length, the swimmers pass for the second time just 10.5 from the shallow end. How long is the pool?

Answer 1

Hint: In this question, we first need to assume the length of the pool as some x and then find the distance of both the swimmers when they pass the first time and then find the distance traveled from the other end when they pass again. Now, the rate at which the distances covered should be equal as their respective speeds are constant which gives a quadratic equation in x. Then on simplifying it further we get the result.

Complete step by step answer:
Let us assume the length of the pool as x
Now, given that at the same time when B covers a distance of 18.5 then A covers \[x-18.5\] for the first time they pass from the deep end

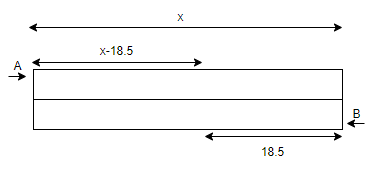
Now, again in the same time B covers a distance of \[x-18.5+10.5\]now from the shallow end and so A covers a distance of \[18.5+x-10.5\]

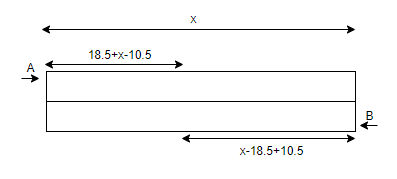
Here, as the speeds of the respective swimmers remains constant so the rate of distance travelled by them also remains the same which can be further written as
\[\Rightarrow \dfrac{18.5}{x-18.5}=\dfrac{x-8}{x+8}\]
Now, on cross multiplying further we get,
\[\Rightarrow 18.5\left( x+8 \right)=\left( x-8 \right)\left( x-18.5 \right)\]
Now, this can be further written in the simplified form as
\[\Rightarrow 18.5x+148={{x}^{2}}-8x-18.5x+148\]
Now, on cancelling the common terms and rearranging we get,
\[\Rightarrow {{x}^{2}}=18.5x+8x+18.5x\]
Now, on further simplification we get,
\[\Rightarrow {{x}^{2}}=\]45x
Now, on further cancelling the common term on both sides we get,
\[\therefore x=45\]
Hence, the length of the pool is 45.
Note:
Instead of finding the rate of distances covered, we can also find the speeds using the distance speed and time relation and then equate accordingly. Both methods give the same result.
It is important to note that when they pass for the second time the distance covered by them should be including both the distance covered before and now and also to be noted that the first time it is from the deep end and the second time it is from the shallow end.