
A and B are two points separated by a distance 5cm. Two charges \[10\mu C\text{ and }20\mu C\] are placed at A and B. The resultant electric intensity at a point P outside the charges at a distance 5cm from \[10\mu C\] is –
\[\begin{align}
& \text{A) 54}\times \text{1}{{\text{0}}^{6}}N{{C}^{-1}}\text{ away from 10}\mu C \\
& \text{B) 56}\times \text{1}{{\text{0}}^{6}}N{{C}^{-1}}\text{ towards 10}\mu \text{C} \\
& \text{C) 9}\times \text{1}{{\text{0}}^{6}}N{{C}^{-1}}\text{ away from 10}\mu \text{C} \\
& \text{D) Zero} \\
\end{align}\]
Answer
574.2k+ views
Hint: We need to consider the given system with the charges and the point P to be in a single line. We can take the point to be at a distance of 5 cm from the charge A with which the solution is to be compared with. The total electric field can be found easily.
Complete step by step solution:
Let us consider the situation given to us. Two charges are kept 5 cm away from each other and we have to find the electric field intensity at a point P which is outside the system as shown in the figure given below.
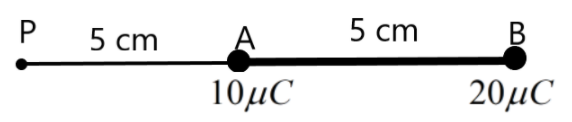
We are to find the electric field intensity at the point P. We know that the point P will have the electric field due to the charges at both the points A and B. We can find the individual electric field intensities due to each charge at the point P.
The electric field intensity at P due to the charge A of charge \[10\mu C\] at a distance of 5 am from P can be given as –
\[\begin{align}
& E=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{Q}{{{r}^{2}}} \\
& \Rightarrow {{E}_{AP}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{10\times {{10}^{-6}}}{{{(5\times {{10}^{-2}})}^{2}}} \\
& \Rightarrow {{E}_{AP}}=\dfrac{9\times {{10}^{9}}\times {{10}^{-5}}}{25\times {{10}^{-4}}} \\
& \Rightarrow {{E}_{AP}}=\dfrac{9}{25}\times {{10}^{8}}N{{C}^{-1}} \\
\end{align}\]
Similarly, the electric field at P due to charge B which is 10cm away from P is given as –
\[\begin{align}
& E=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{Q}{{{r}^{2}}} \\
& \Rightarrow {{E}_{BP}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{20\times {{10}^{-6}}}{{{(10\times {{10}^{-2}})}^{2}}} \\
& \Rightarrow {{E}_{BP}}=\dfrac{9\times {{10}^{9}}\times 2\times {{10}^{-5}}}{100\times {{10}^{-4}}} \\
& \Rightarrow {{E}_{BP}}=\dfrac{18}{100}\times {{10}^{8}}N{{C}^{-1}} \\
\end{align}\]
Now, we can find the total electric field at P as the sum of the fields due to A and B as –
\[\begin{align}
& {{E}_{P}}={{E}_{AP}}+{{E}_{BP}} \\
& \Rightarrow {{E}_{P}}=\dfrac{9}{25}\times {{10}^{8}}N{{C}^{-1}}+\dfrac{18}{100}\times {{10}^{8}}N{{C}^{-1}} \\
& \Rightarrow {{E}_{P}}=\dfrac{36+18}{100}\times {{10}^{8}}N{{C}^{-1}} \\
& \therefore {{E}_{P}}=54\times {{10}^{6}}N{{C}^{-1}} \\
\end{align}\]
Also, we can understand that the direction of the electric field will be away from the point A.
So, the required answer is given by option A.
Note:
The electric field at different points will be different. The point P which we have considered is along the axis that connects the two charges which made our calculations pretty much easier. In other cases, we need to consider the angles involved between them.
Complete step by step solution:
Let us consider the situation given to us. Two charges are kept 5 cm away from each other and we have to find the electric field intensity at a point P which is outside the system as shown in the figure given below.
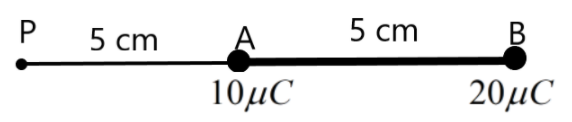
We are to find the electric field intensity at the point P. We know that the point P will have the electric field due to the charges at both the points A and B. We can find the individual electric field intensities due to each charge at the point P.
The electric field intensity at P due to the charge A of charge \[10\mu C\] at a distance of 5 am from P can be given as –
\[\begin{align}
& E=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{Q}{{{r}^{2}}} \\
& \Rightarrow {{E}_{AP}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{10\times {{10}^{-6}}}{{{(5\times {{10}^{-2}})}^{2}}} \\
& \Rightarrow {{E}_{AP}}=\dfrac{9\times {{10}^{9}}\times {{10}^{-5}}}{25\times {{10}^{-4}}} \\
& \Rightarrow {{E}_{AP}}=\dfrac{9}{25}\times {{10}^{8}}N{{C}^{-1}} \\
\end{align}\]
Similarly, the electric field at P due to charge B which is 10cm away from P is given as –
\[\begin{align}
& E=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{Q}{{{r}^{2}}} \\
& \Rightarrow {{E}_{BP}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{20\times {{10}^{-6}}}{{{(10\times {{10}^{-2}})}^{2}}} \\
& \Rightarrow {{E}_{BP}}=\dfrac{9\times {{10}^{9}}\times 2\times {{10}^{-5}}}{100\times {{10}^{-4}}} \\
& \Rightarrow {{E}_{BP}}=\dfrac{18}{100}\times {{10}^{8}}N{{C}^{-1}} \\
\end{align}\]
Now, we can find the total electric field at P as the sum of the fields due to A and B as –
\[\begin{align}
& {{E}_{P}}={{E}_{AP}}+{{E}_{BP}} \\
& \Rightarrow {{E}_{P}}=\dfrac{9}{25}\times {{10}^{8}}N{{C}^{-1}}+\dfrac{18}{100}\times {{10}^{8}}N{{C}^{-1}} \\
& \Rightarrow {{E}_{P}}=\dfrac{36+18}{100}\times {{10}^{8}}N{{C}^{-1}} \\
& \therefore {{E}_{P}}=54\times {{10}^{6}}N{{C}^{-1}} \\
\end{align}\]
Also, we can understand that the direction of the electric field will be away from the point A.
So, the required answer is given by option A.
Note:
The electric field at different points will be different. The point P which we have considered is along the axis that connects the two charges which made our calculations pretty much easier. In other cases, we need to consider the angles involved between them.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




