Question

A and B are two persons sitting in a circular arrangement with \[8\] other persons. Find the probability that both \[A\] and \[B\;\] sit together.

Answer 1

Hint: First, we have to define what the terms we need to solve the problem are. The number of people given in this question is \[8\]plus the two others are sitting in a circular arrangement Thus, the total number of people is $10$. We will take the possibility of the two persons sitting on either side of the \[8\] other persons to interchange their seats.

Complete answer:

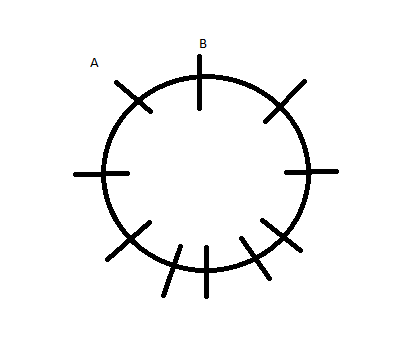
Now the number of persons in the given question is $10$( two persons sitting in a circular arrangement with \[8\] other persons).
So total number of including $A,B$ is $8 + 2 = 10$
Permutation is a way of changing or arranging the elements or objects in a linear order. The formula for permutation for n objects taken r at a time is given by \[P\left( {n,r} \right){\text{ }} = {\text{ }}\dfrac{{n!}}{{\left( {n - r} \right)!}}\]
As this a case of circular permutations, ten people randomly be arranged around a circular table in$(n - 1)!$hence applying the know values in the formula we get $(n - 1)! = (10 - 1)! = 9!$ ways
Since two particular people are always together, so consider them as one person and let it be saying $P$
Now $P$ with others \[8\], so $9$ can arrange around the table in $8!$ways (as arranged around a circular table is$(n - 1)!$) also the two between themselves can arrange in $2!$ways.
Hence the required probability is $\dfrac{{8! \times 2!}}{{9!}}$$\dfrac{{8! \times 2!}}{{9 \times 8!}} = \dfrac{2}{9}$(since $9!$ can be written as $9 \times 8!$ and canceling each other)
Therefore, the probability for both \[A\] and \[B\;\] sit together is $\dfrac{2}{9}$


Note: For probability first, determine a single event with a single outcome and identify the total number of outcomes that can occur then finally divide the number of events by the number of possible outcomes.
Which is \[Probability = \dfrac{{{\text{ }}number{\text{ }}of{\text{ }}favourable{\text{ }}outcomes}}{{total{\text{ }}number{\text{ }}of{\text{ }}outcome}}\].