Question

(a) A school auditorium is \[50\,m\] long and \[30\,m\] wide. This auditorium is surrounded by a verandah 5m wide on the outside of it. Find the area of the verandah. If tiles of \[50{\text{ }}cm{\text{ }} \times {\text{ }}50{\text{ }}cm\] are fixed on the verandah, how many tiles will it require.
(b) The outer length and breadth of a photo frame is \[60\;cm{\text{ }} \times {\text{ }}40{\text{ }}cm\] . If the width of the frame is 2.5 cm, what is the length and breadth of the picture that will be visible?

Answer 1

Hint: Find the total area and subtract it from the area of the auditorium.
First, we are going to find the total area of the given figure and when we find it, then we will find the inner rectangle which is the area of auditorium, after finding this we will subtract it from the total area and get the area of verandah and then we will find the area of each tiles and then find the total number of tiles required. We have subtracted total length and breadth from the side of the frame which gets us the required solution.

Complete step by step solution:
Below is the diagrammatic representation of the problem (a)

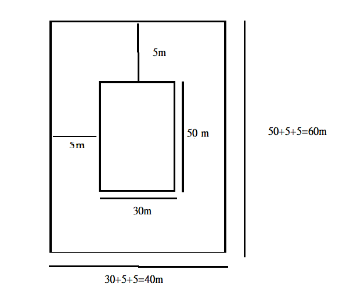
First, we have to find the total area of the given figure, to find that we have to find the sides, we get
The sides as $ 60\;m\,and\,\,40\,m $ , Now we can find the total area
 $ Area = 60 \times 40 = 2400\;{m^2} $
Now, we have to find the inner rectangle which is the auditorium
 $ Area = 50 \times 30 = 1500\;{m^2} $
Now, we can find the area of verandah
 \[
  Area{\text{ }}of{\text{ }}verandah = {\text{ }}Total{\text{ }}area{\text{ }} - area{\text{ }}of{\text{ }}auditorium \\
  Area = 2400 - 1500 = 900\;{m^2} \;
\]
Now, we have the area of verandah, now we can find the total tiles required.
So, area of each tile is $ = 50 \times 50 = 2500c{m^2} = 0.25\;{m^2} $
So, the total tiles required area = $ \dfrac{{Area\,\,of\,verandah}}{{area\,of\,tile}} $
 $
   = \dfrac{{900}}{{0.25}} \\
   = 3600 \;
 $
Therefore, the total tiles required are 3600 tiles.

(b) Diagrammatic representation

 \[
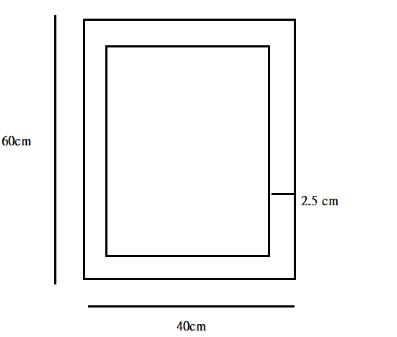
  Length = 60 - (2.5 + 2.5) \\
   = 60 - 5 \\
   = 55\;cm \;
\]
 $
  Breadth = 40 - (2.5 + 2.5) \\
   = 40 - 5 \\
   = 35\;cm \;
  $
Therefore, we have found the length and breadth of the visible picture.

Note: When we are going to find the total area, we have to add the side of auditorium and the sides of verandah such that we get the total which gives us the length of the total figure which is required for finding the area of total figure and in the similar way we have to subtract total length and breadth of total with the width of the frame.