Question

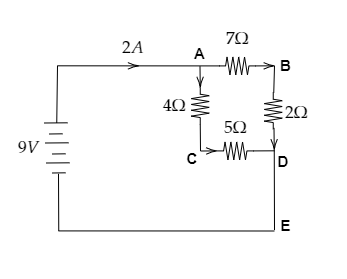
A $9{\text{V}}$ battery is connected to four resistors to form a simple circuit as shown in the figure. How would the current through the $2\Omega $ resistor compare to the current through the $4\Omega $ resistor?

A) One – fourth as large
B) One – half as large
C) Four times as large
D) Equally as large

Answer 1

Hint:In the given figure the four resistors can be viewed as two branches of equivalent resistances. Each branch is made up of two resistors connected in series. Then using Ohm’s law the current in the required resistors could be obtained and compared.

Formula used:
-Ohm’s law gives the current through a resistor as $I = \dfrac{V}{R}$ where $V$ is the potential difference across the resistor and $R$ is the resistance of the resistor.
-The equivalent resistance of two resistors in series connection is given by, ${R_{eq}} = {R_1} + {R_2}$ where ${R_1}$ and ${R_2}$ are the resistances of the two resistors.

Complete step by step answer.
Step 1: Sketch the circuit diagram given in the question.

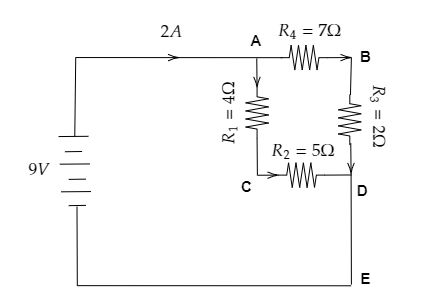
In the above circuit diagram, we split the four resistors into two branches namely branch ACD and branch ABD. We chose these branches as these consist of resistors in series and the direction of current flow is continuous through each resistor of the same branch.
The voltage of the battery is $V = 9{\text{V}}$ and the current through the circuit is $I = 2{\text{A}}$ .
From the figure, we have the resistance across AC as ${R_1} = 4\Omega $, the one across CD is ${R_2} = 5\Omega $, the one across BD is ${R_3} = 2\Omega $ and finally, the resistance across AB is ${R_4} = 7\Omega $ .
Step 2: Obtain the equivalent resistance in each branch.
As seen from the figure, in branch ACD, ${R_1}$ and ${R_2}$ are connected in series.
So their equivalent resistance is given by, ${R_{ACD}} = {R_1} + {R_2}$ -------- (1)
Substituting for ${R_1} = 4\Omega $ and ${R_2} = 5\Omega $ in equation (1) we get, ${R_{ACD}} = 4 + 5 = 9\Omega $
Thus the equivalent resistance of branch ACD is ${R_{ACD}} = 9\Omega $ .
In branch ABD, ${R_3}$ and ${R_4}$ are connected in series.
So their equivalent resistance is given by, ${R_{ABD}} = {R_3} + {R_4}$ -------- (2)
Substituting for ${R_3} = 2\Omega $ and ${R_4} = 7\Omega $ in equation (2) we get, ${R_{ABD}} = 2 + 7 = 9\Omega $
Thus the equivalent resistance of branch ABD is ${R_{ABD}} = 9\Omega $ .
Thus the effective resistance of each branch is the same.
i.e., ${R_{ACD}} = {R_{ABD}} = 9\Omega $ .
Step 3: Determine the current through each branch.
The reduced circuit is given below.

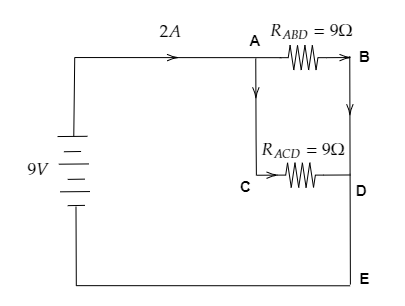
The resistance ${R_{ACD}}$ and ${R_{ABD}}$ are connected in parallel.
Ohm’s law gives the current through ${R_{ACD}}$ as ${I_{ACD}} = \dfrac{V}{{{R_{ACD}}}}$ ------- (3)
Substituting for $V = 9{\text{V}}$ and ${R_{ACD}} = 9\Omega $ in equation (3) we get, ${I_{ACD}} = \dfrac{9}{9} = 1{\text{A}}$
Thus the current through ${R_{ACD}}$ is ${I_{ACD}} = 1{\text{A}}$ .
The current through ${R_{ABD}}$ will be ${I_{ACD}} = {I_{ABD}} = 1{\text{A}}$ as the two resistances are equal.
Step 4: Now determine the current through each resistor in the two branches using the obtained values of current through the two branches.
Here as in each branch, the corresponding two resistors are connected in series, the current through each resistor of a particular branch will be the same as the current through the branch resistance.
i.e., ${I_1} = {I_2} = {I_{ACD}} = 1{\text{A}}$ and ${I_3} = {I_4} = {I_{ABD}} = 1{\text{A}}$ .
So the current through ${R_1} = 4\Omega $ and${R_3} = 2\Omega $ is the same.

So the correct option is D.

Note:When resistors are connected in series, the current through each resistor will be the same but the potential difference across each resistor will be different. When resistors are connected in parallel, the potential difference across each resistor will be the same but the current through each resistor will be different.