Question

A $ 60kg $ painter stands on a $ 15kg $ platform. A rope attached to the platform and passing over an overhead pulley allows the painter to raise himself along with the platform. What force must he exert on the rope so as to attain an upward speed of $ 1m{s^{ - 1}} $ in $ 1s $ ?

 $ A)400N \\
  B)325N \\
  C)412.5N \\
  D)620.5N \\ $

Answer 1

Hint :A force is any interaction that, while unopposed, causes an object to change its motion. A force may cause a mass object to change its velocity (which involves starting to move from a standstill), that is to accelerate.

Complete Step By Step Answer:
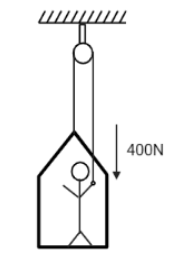
As seen in the figure, the painter's free body diagram and the platform as a structure can be drawn. It's worth noting that the string's tension is equal to the force with which he pulls the rope.
The acceleration must be $ 1m{s^{ - 2}} $ to achieve a speed of $ 1m{s^{ - 1}} $ in one second.
Therefore, we get,
 $ 2F - \left( {M + m} \right)g = \left( {M + m} \right)a $
Now we take $ \left( {M + m} \right)g $ to the right hand side,
 $ 2F = \left( {M + m} \right)g + \left( {M + m} \right)a $ ,
Since $ \left( {M + m} \right) $ is common for two terms, we can combine it to form,
 $ 2F = \left( {M + m} \right)\left( {g + a} \right) $
On solving for $ F $ , we get,
 $ F = \dfrac{1}{2}\left( {M + m} \right)\left( {g + a} \right) $
From the question, we know that, $ F $ represents the applied force,
 $ M = 60kg $ represents the mass of the painter,
 $ m = 15kg $ represents the mass of the platform,
 $ g = 10m{s^{ - 2}} $ represents the acceleration due to gravity, and
 $ a = 1m{s^{ - 2}} $ represents the acceleration.
Now, we substitute these values to the formula,
 $ F = \dfrac{1}{2}\left( {M + m} \right)\left( {g + a} \right) \\
   = \dfrac{1}{2}\left( {60 + 15} \right)\left( {10 + 1} \right) \\
   = \dfrac{1}{2}\left( {75} \right)\left( {11} \right) \\
   = \dfrac{1}{2}\left( {825} \right) \\
   = 412.5 \\ $
Thus, the applied force $ F = 412.5N $ and therefore the correct option is $ C)412.5N $ .

Note :
Since acceleration is characterised as a change in velocity over time, it is maximum when velocity is zero. For anything to accelerate, there must be a change in velocity. To put it another way, if anything is speeding up, it must have a variable velocity. The acceleration is zero if the velocity is constant (because the velocity does not change over time).