Question

A 60Hp electric motor lifts an elevator having a maximum load capacity of $2000kg$. If the frictional force on the elevator is 4000N, the speed of the elevator at full load is close to: $(1Hp=746watt, g=10m{{s}^{-2}})$
$\begin{align}
  & \text{A}\text{. }1.5m{{s}^{-1}} \\
 & \text{B}\text{. }1.9m{{s}^{-1}} \\
 & \text{C}\text{. }1.7m{{s}^{-1}} \\
 & \text{D}\text{. 2}\text{.0}m{{s}^{-1}} \\
\end{align}$

Answer 1

Hint: Power is the rate of doing work. Commercial unit of power is horsepower. First convert horsepower to watt.Now calculate total force on the elevator which will be the sum of the weight and the frictional force. As power is also defined as the product of force and velocity. So equate the maximum Power to product of the force on the elevator and the velocity. Form that finds the velocity of the elevator at full load.
Formulas used: Total force on the body is
$F=\text{ Weight at maximum load + Frictional Force}$
Power ,$P=\overrightarrow{F}.\overrightarrow{v}=Fv\cos \theta $
Where,$v=\text{Velocity}$,$\theta =\text{ angle between the force and velocity}$
Weight of an object of mass $m$is $W=\text{mass }\times \text{ acceleration due to gravity=}mg$

Complete step-by-step solution:
Given that, $1Hp=746watt,g=10m{{s}^{-2}}$ and frictional force on the elevator is $f=4000N$, maximum load $m=2000kg$

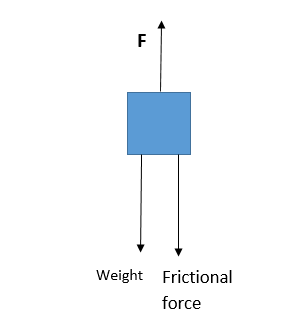
The power of the electric motor which lifts the elevator is $60Hp$and its maximum load is $2000kg$.
From the free body diagram the total force on the elevator at maximum load is
$\begin{align}
  & F=\text{ Weight at maximum load + Frictional Force} \\
 & \Rightarrow F=\text{ Maximum mass }\times \text{ acceleration due to gravity + Frictional force=}mgf \\
 & \Rightarrow F=2000\times 10+4000=24000N \\
\end{align}$
But we know power generated is the dot product of Force and velocity.so
$P=\overrightarrow{F}.\overrightarrow{v}=Fv\cos \theta $
From free body diagram the angle between the force and the velocity is zero so
$P=Fv\text{ , or, }v=\dfrac{P}{F}$
Maximum power generated by the engine is $P=60Hp=60\times 746watt=44760watt$
And maximum force is, $F=24000N$
So the velocity of the elevator at full load is
$v=\dfrac{P}{F}=\dfrac{44760}{24000}=1.866\simeq 1.9m{{s}^{-1}}$
So the correct option is $\text{B}\text{. }1.9m{{s}^{-1}}$.

Note: For problems like this first draw the free body diagram. Then for equilibrium condition calculate the forces. From the force you can calculate work done by the force and also power delivered. Also note that the S.I unit of power is not $Hp$. $Hp$ stands for “Horse-power” which is a relative term invented by James Watt to compare the output of engines with the output of a horse. Also the S.I unit of power i.e. watt is very small so commercially we use a bigger unit of power which is Horse-power.