Question

A $5{\text{kg}}$ mass falls through $400{\text{cm}}$. Find the work done on it by the earth’s gravitational force.
A) $196{\text{J}}$
B) $1960{\text{J}}$
C) $980{\text{J}}$
D) $19 \cdot 6{\text{J}}$

Answer 1

Hint:As a body falls through a height, the force acting on the body will be the force due to gravity also known as the weight of the body. Work done by this force will be the dot product of the force acting on the body and the displacement i.e. the height through which it falls.

Formulas used:
-The work done by the force acting on a body is given by, $W = F \cdot d$ where $F$ is the force acting on the body and $d$ is the displacement of the body.
-The force due to gravity is given by, ${F_g} = mg$ where $m$ is the mass of the body and $g$ is the acceleration due to gravity.

Complete step by step answer.
Step 1: List the parameters given about the problem at hand.

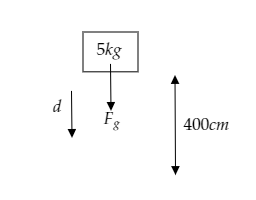
The mass of the body is given to be $m = 5{\text{kg}}$ .
The height through which it falls or the magnitude of the displacement of the body is given to be $d = 400{\text{cm}}$ .
Let $g = 9 \cdot 8{\text{m}}{{\text{s}}^{ - 2}}$ be the acceleration due to gravity.
We have to determine the work done by the earth’s gravitational force.
Step 2: Express the relation for the force acting on the body.
The force due to gravity or the weight of the body can be expressed as ${F_g} = mg$ -------- (1)
Substituting for $m = 5{\text{kg}}$ and $g = 9 \cdot 8{\text{m}}{{\text{s}}^{ - 2}}$ in equation (1) we get, ${F_g} = 5 \times 9 \cdot 8 = 49{\text{N}}$ .
Thus the force acting on the body is ${F_g} = 49{\text{N}}$ .
Step 3: Express the relation for the work done by the earth’s gravitational force.
The work done by the earth’s gravitational force acting on the given body can be expressed as $W = {F_g} \cdot d = {F_g}d$ -------- (2)
Substituting for ${F_g} = 49{\text{N}}$ and $d = 4{\text{m}}$ in equation (2) we get, $W = 49 \times 4 = 196{\text{J}}$ .
$\therefore $ the work done on the body is $W = 196{\text{J}}$ .

So the correct option is A.

Note:While substituting values of physical quantities in any equation, make sure that all the quantities are expressed in their respective S.I units. Here the displacement of the body was expressed in centimetres so we converted it into meters as $d = 4{\text{m}}$ before substituting in equation (2). Since the force due to gravity and the displacement are in the same direction, the dot product becomes the product of force and displacement in equation (2). The potential energy of the body at the given height before falling is the work done by the earth’s gravitational force.