Question

A $55\,kg$ man holds a weight of $20\,kg$ on his head. What is the work done by him against gravity if he moves a distance of $20\,m$
(i) On a horizontal road
(ii) On an incline of $1$ in $5$?
Take $g = 10\,m{s^{ - 2}}$.

Answer 1

Hint: In order to solve this problem we should first get some idea about work done. Work is a physics term that describes the energy transfer that occurs when an object is moved over a distance by an external force that is applied in at least part of the displacement direction.

Formula used:
Work done, $W = FS\cos \theta .$
Where, $F$ is force ,$S$ is displacement and $\theta $ is the angle between $F\,and\,S.$

Complete step-by-step solution:
 So let us solve the first bit of the problem:
(i). So as given in the problem that man holds a weight on his head.

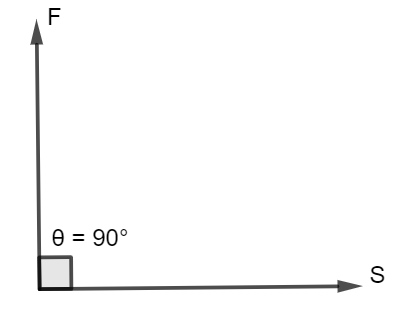
So from the diagram we can understand that the man applies force on the weight in the upward direction and moving in the horizontal direction and angle between them is ${90^ \circ }$.
So as we know
$W = FS\cos \theta .$
And here $\theta = {90^ \circ }$ and $\cos \,{90^ \circ } = 0$
$\therefore Work\,done\,(W) = 0.$
(ii). Lets us see the diagram for this part

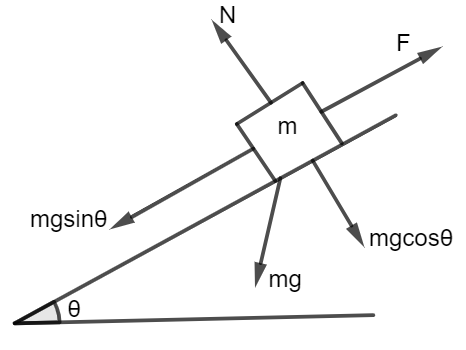
As we can see from the diagram
$m = 55\,kg + 20\,kg = 75\,kg$
$N = mg\cos \theta $
$F = mg\sin \theta $
Direction of displacement is the same in the $F$ direction.
So, the angle between $F\,and\,S$ is ${0^ \circ }$
$W = FS\cos \theta .$
Displacement $S = 20\,m$ is given in the problem and incline is $1$ in $5$means $\sin \theta = \dfrac{1}{5}$
$W = mg\sin \theta \times (20) \times \cos {0^ \circ }$
$W = 75 \times 10 \times \dfrac{1}{5} \times 20$
$W = 3000J$

Note: In order to solve this problem there are some important points which we should keep on our fingertips. Resolving the vector component is important to understand about force direction. And remember the work done formula and understanding about the angles.