Question

A 45kg traffic light is suspended with two steel wires of equal lengths and radii of\[0.5cm\] . if the wires make an angle of \[15^\circ \] with the horizontal, what is the fractional increase in their length due to the weight of the light? Given, Young’s modulus of steel = $2.0 \times {10^{11}}N{m^{ - 2}}$

Answer 1

Hint: At first, a free body diagram has to be drawn and denote the forces acting on the system. Next, the tension of the wires has to be calculated from the given values. Use the formula of young’s modulus and find the increase in length of the wire due to the tension. Note that, in the place of force in the formula use the value of tension that is gained from the diagram.
Formula used:
The tension is divided into two components: horizontal and vertical. Hence, we get
$2T\sin \theta = mg$
$m$ is the mass of the traffic light, $T$ is the tension of the wire, the wires make an angle of \[\theta \] with the horizontal.
The formula of Young’s modulus , $Y = \dfrac{F}{{A\left( {\dfrac{{\Delta l}}{l}} \right)}}$
$F = $ The force acting on the wires= $T$ (The tension of the wire)
$A = $ The cross-sectional area of the wire.
$\left( {\dfrac{{\Delta l}}{l}} \right) = $ The fractional increase in the length of the wire due to the weight of the light.

Complete step-by-step solution:
Let us draw the free body diagram regarding the problem,

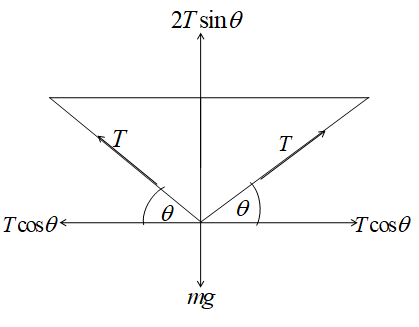
From the diagram, we get $2T\sin \theta = mg$
$ \Rightarrow T = \dfrac{{mg}}{{2\sin \theta }}$
Given, $m = 45kg$, $g = 9.8m/{s^2}$ , $\theta = 15^\circ $
$ \Rightarrow T = \dfrac{{45 \times 9.8}}{{2\sin 15}}$
$ \Rightarrow T = \dfrac{{45 \times 9.8}}{{2 \times 0.65}}$
$ \Rightarrow T = \dfrac{{441}}{{1.3}}$
$ \Rightarrow T = 339.23N$
The formula of Young’s modulus , $Y = \dfrac{F}{{A\left( {\dfrac{{\Delta l}}{l}} \right)}}$
$Y = 2.0 \times {10^{11}}N{m^{ - 2}}$
$F = $ the force acting on the wires= $T$( the tension of the wire)
$ \Rightarrow F = 339.23N$
$A = $ the cross-sectional area of the wire.
$ \Rightarrow A = \pi {r^2}$ , $r = 0.5cm = \dfrac{{0.5}}{{100}}m$
$ \Rightarrow A = \pi {\left( {\dfrac{{0.5}}{{100}}} \right)^2} = 7.85\times {{10}^{ - 5}}{m^2}$
$\left( {\dfrac{{\Delta l}}{l}} \right) = $ the fractional increase in the length of the wire due to the weight of the light.
$ \Rightarrow \left( {\dfrac{{\Delta l}}{l}} \right) = \dfrac{F}{{YA}}$
$ \Rightarrow \left( {\dfrac{{\Delta l}}{l}} \right) = \dfrac{{339.23}}{{2.0 \times {{10}^{11}} \times 7.85 \times {{10}^{ - 5}}}}$
$ \Rightarrow \left( {\dfrac{{\Delta l}}{l}} \right) = 2.16 \times {10^{ - 5}}$
Hence, the fractional increase in the length of the wire due to the weight of the light $ = 2.16 \times {10^{ - 5}}$(answer)

Note: Young's modulus is described as the mechanical characteristic of a material to withstand the compression or the elongation concerning its actual length. It is denoted as Y. It is also a fact that many matters are non-linear and elastic over a little amount of deformation. Its unit is Pascal and dimension \[[M{L^ - }^1{T^ - }^2]\] .