Question

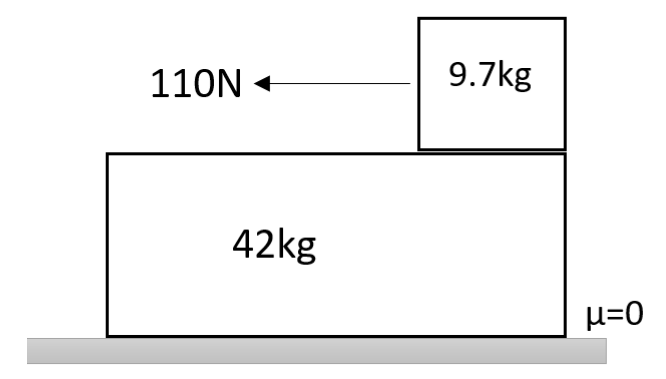
A $42kg$ slab rests on a frictionless floor. A $9.7kg$ block rests on the top side of the slab as shown in the diagram. The coefficient of static friction between the block and the slab is given as $0.53$, while the coefficient of kinetic friction is given as $0.43$. The block of mass $9.7kg$ is acted upon by a horizontal force of $110N$. What will be the resulting accelerations of
(a) The block.
(b) The slab.

Answer 1

Hint: First of all find the static frictional force and the kinetic frictional force accordingly. Then find the acceleration of the slab by dividing the kinetic frictional force by the mass of the slab. And then the acceleration of the block has to be found by dividing the difference between the force acting and the kinetic frictional force by the mass of the block.

Complete step by step answer:

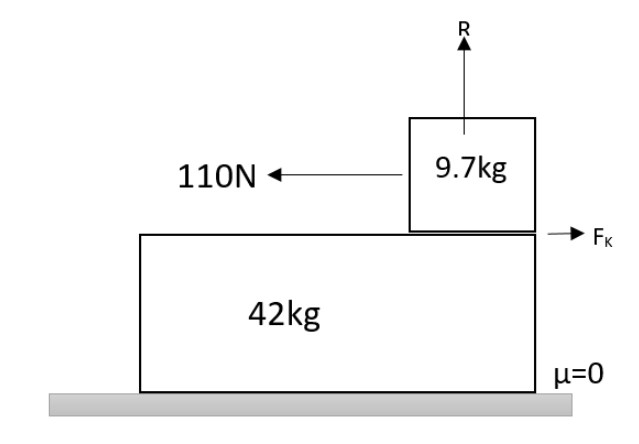
The static frictional force can be found by the equation,
${{F}_{S}}={{\mu }_{S}}\times R$
Where ${{\mu }_{S}}$ be the coefficient of static friction and $R$ be the normal reaction of the force acting.
It is given that the coefficient of static friction is,
${{\mu }_{S}}=0.53$
And the normal reaction can be calculated as,
$R=m\times g$
Where $m$be the mass of the block and $g$ be the acceleration due to gravity.
The mass of the block is given as,
$m=9.7kg$
Acceleration due to gravity is,
$g=10m{{s}^{-2}}$
Substituting this in the equation of normal reaction will give,
$R=9.7\times 10=97N$
Therefore the static frictional force will be,
${{F}_{S}}=0.53\times 97=51.41N$
Now the kinetic force of friction will be,
${{F}_{K}}={{\mu }_{K}}\times R$
Where ${{\mu }_{K}}$ be the coefficient of kinetic friction given as,
${{\mu }_{K}}=0.43$
Substituting the values in this equation will give,
${{F}_{K}}=0.43\times 97=41.71N$
The acceleration of the slab is given by the equation,
${{a}_{s}}=\dfrac{{{F}_{K}}}{M}$
Where $M$be the mass of the slab given as,
$M=42kg$
Substituting the values in it,
${{a}_{s}}=\dfrac{41.71}{42}=0.993m{{s}^{-2}}$
Therefore the acceleration of the block will be given as,
${{a}_{B}}=\dfrac{F-{{F}_{K}}}{m}$
Where $F$be the force acting on the block.
Substituting the values in this equation will give,
${{a}_{B}}=\dfrac{110-41.71}{9.7}=7.04m{{s}^{-2}}$

Note: Generally the coefficient of kinetic friction is found to be less than the coefficient of static friction. This frictional force is defined as the force acting in the opposite direction. This will be parallel to the surface also.